It’s long been known that applying linear regression to equations transformed from nonlinear forms is generally not advisable. However, I had never actually examined how much the resulting values might differ in practice—so I decided to test it myself.
There are several methods that transform nonlinear equations into linear ones to estimate parameters. These include:
- Scatchard plot (used in ligand binding assays)
- Lineweaver–Burk plot (used in enzyme kinetics)
- Eadie-Hofstee plot
- Hanes–Woolf plot
Contents
Scatchard Equation and Plot
Derivation
Let’s assume an equilibrium between a receptor and a ligand as follows: $$ [R] + [L] \rightleftharpoons [RL] $$ The dissociation constant \(K_{\rm d}\) is defined as: $$K_{\mathrm d} = \frac{[R][L]}{[RL]} $$ Also, $$[R_{\mathrm T}] = [R] + [RL]$$ So, $$[RL] = \frac{[R_{\mathrm T}][L]}{K_{\mathrm d} + [L]} $$ This equation is a nonlinear expression equivalent to the Michaelis–Menten equation in enzyme kinetics. On the other hand, if we rearrange the same equation, we get: $$ \frac{K_{\mathrm d}[RL]}{[L]} = -[RL] + [R_{\mathrm T}] $$ Dividing both sides by \(K_{\rm d}\): $$\frac{[RL]}{[L]} = -\frac{1}{K_{\mathrm d}}[RL] + \frac{[R_{\mathrm T}]}{K_{\mathrm d}} $$ This is the Scatchard equation, which corresponds to the Eadie–Hofstee plot, a linear representation of the Michaelis–Menten equation.< From this equation, if you plot \([RL]\) on the x-axis and \([RL]/[L]\) on the y-axis, and perform linear regression, you will get a straight line where:
- The slope is \(-1/K_{\rm d}\)
- The x-intercept is \([R_{\rm T}]\)
Problems
The main problems with the Scatchard plot include:
- The x-axis (\([RL]\)) and y-axis (\([RL]/[L\)]) are not independent variables, since both contain \([RL]\).
- Least squares regression is fundamentally not applicable here, because it assumes:
- The x-axis is the explanatory variable (with no experimental error)
- The y-axis is the dependent variable (which contains experimental error)
- You cannot apply the correlation coefficient as a goodness-of-fit indicator.
- The method is indirect and extrapolative, rather than directly estimating parameters.
Practice Problem
I tried solving a practice problem from the lecture material archived at the following URL:
Mg2+ and ADP form a 1:1 complex. In the binding experiment, the total concentration of ADP is kept constant at 80 µM. From the data in the following table, determine the dissociation constant \(K_{\rm d}\).
| Total Mg2+ (µM) | Mg2+ bound to ADP (µM) |
| 20 | 11.6 |
| 50 | 26.0 |
| 100 | 42.7 |
| 150 | 52.8 |
| 200 | 59.0 |
| 400 | 69.5 |
First, from the equation \([RL] = \frac{[R_{\rm T}][L]}{(K_{\rm d} + [L]}\), we know that when \([L] = K_{\rm d}\), \([RL] = \frac{[R_{\rm T}]}{2} = 40\ \mbox{µM}\). So we can estimate that the \(K_{\rm d}\) is roughly around this value.
We analyze the data using R:。
# R Software > TotalMg = c(20, 50, 100, 150, 200, 400) # Total Mg2+ > B = c(11.6, 26.0, 42.7, 52.8, 59.0, 69.5) # Bound Mg<sup>2+</sup>, i.e., [RL] > F = TotalMg - B # Free Mg²⁺, i.e., [L] # Nonlinear regression > result_nonlinear = nls(B ~ Rt*F/(Kd + F), start=c(Rt=10, Kd=10)) > summary(result_nonlinear)Output:
Formula: B ~ Rt * F/(Kd + F)
Parameters:
Estimate Std. Error t value Pr(>|t|)
Rt 79.92642 0.08296 963.5 6.96e-12 ***
Kd 49.86861 0.15975 312.2 6.32e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.05816 on 4 degrees of freedom
Number of iterations to convergence: 5
Achieved convergence tolerance: 1.579e-06
> confint(result_nonlinear)
Waiting for profiling to be done...
2.5% 97.5%
Rt 79.69637 80.15752
Kd 49.42630 50.31459
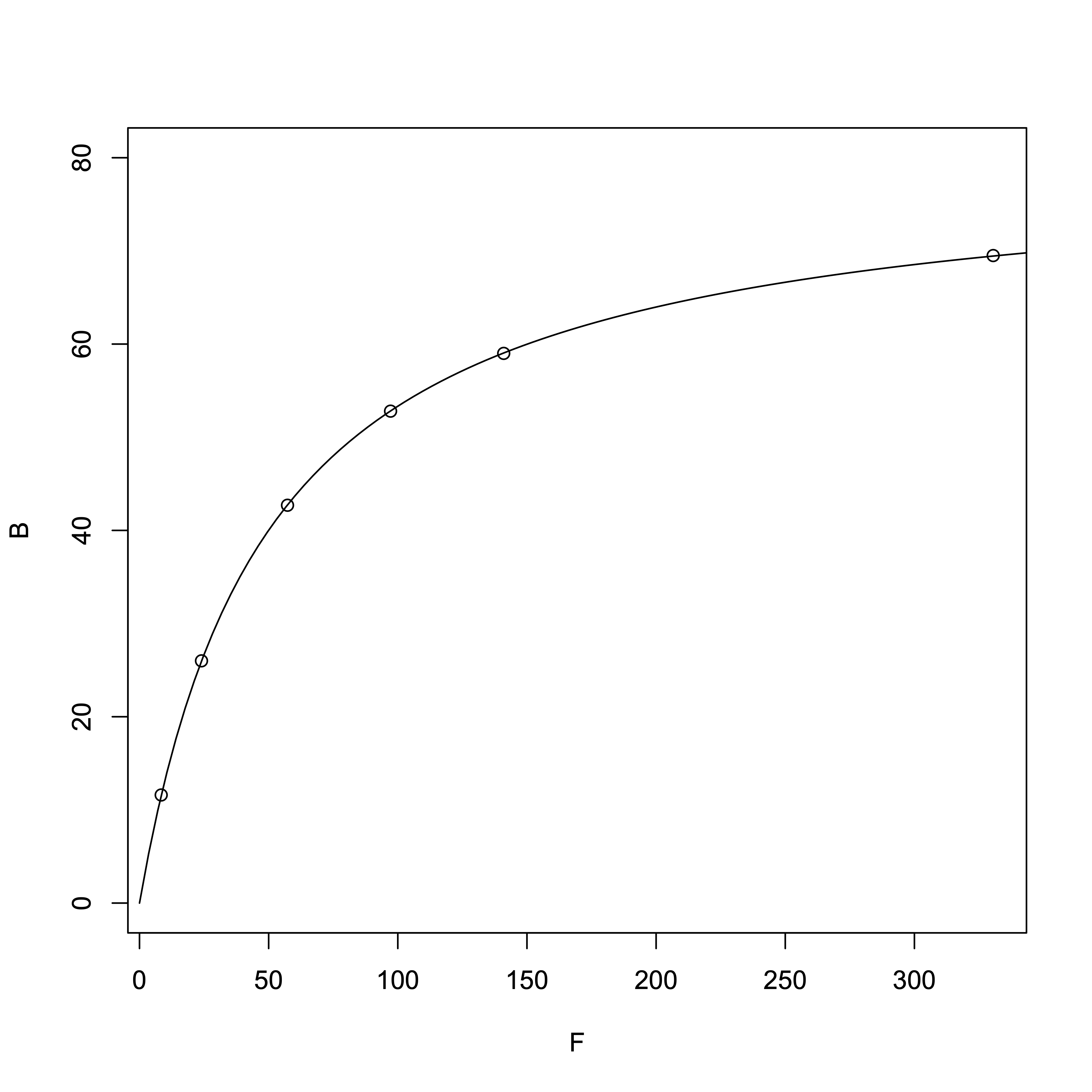
From the nonlinear regression, we obtained:
- Dissociation constant \(K_{\rm d}\) = 49.87 µM
- \([R_{\rm T}]\) = 79.93 µM
Now, using the Scatchard plot to determine \(K_{\rm d}\) and \([R_{\rm T}]\):
# R Software > result_linear = lm(B/F ~ B) > summary(result_linear)Output:
Call:
lm(formula = B/F ~ B)
Residuals:
1 2 3 4 5 6
0.0038911 -0.0026571 -0.0032285 -0.0010654 -0.0005134 0.0035734
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.6115350 0.0033919 475.1 1.18e-10 ***
B -0.0202132 0.0000709 -285.1 9.08e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.00342 on 4 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 0.9999
F-statistic: 8.128e+04 on 1 and 4 DF, p-value: 9.081e-10
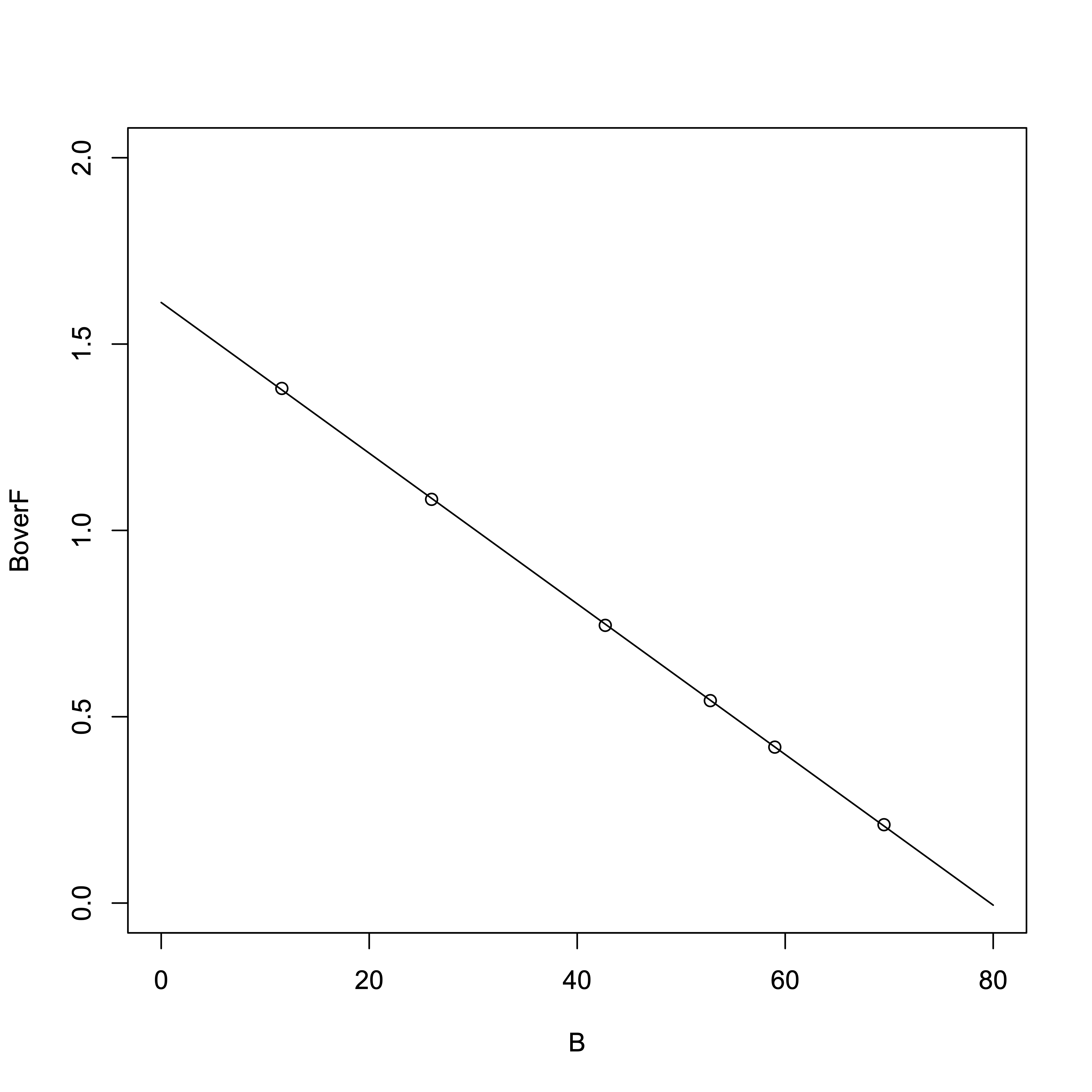
From the regression line:
- Slope = \(-1/K_{\rm d}\) = -0.0202132
- x-intercept (i.e., \([R_{\rm T}]\)) = –y-intercept / slope = 1.6115350 / 0.0202132
- \(K_{\rm d}\) = 49.47 µM
- \([R_{\rm T}]\) = 79.72 µM
This exercise used \(K_{\rm d}\) = 50 µM to generate the data points. However, rounding of the bound Mg2+ values introduces small errors, which result in slight differences in the \(K_{\rm d}\) and \([R_{\rm T}]\) values obtained via nonlinear regression and the Scatchard method. When you calculate using values rounded to the second decimal place, you get results very close to the theoretical ones:
- Nonlinear regression: \(K_{\rm d}\) = 49.99 µM
- Scatchard method: \(K_{\rm d}\) = 49.97 µM
Actual Data
In the previous practice problem using idealized values, there was almost no difference between the results obtained via nonlinear regression and the Scatchard plot. Now, I tried applying both methods to real experimental data to see how they compare.
> B = c(0.729,0.805,0.748,1.328,1.317,1.314,1.905,1.936,1.851,2.546,2.414,2.355) # Units: nM > F = c(6.102,5.532,5.490,10.448,11.710,11.092,22.863,24.570,24.401,48.750,46.621,46.682) # Units: nM > result = nls(B~Rt*F/(Kd+F),start=c(Rt=3,Kd=0.2)) > summary(result)Output:
Formula: B ~ Rt * F/(Kd + F)
Parameters:
Estimate Std. Error t value Pr(>|t|)
Rt 3.3825 0.1127 30.01 3.95e-11 ***
Kd 18.3799 1.4360 12.80 1.59e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.06848 on 10 degrees of freedom
Number of iterations to convergence: 6
Achieved convergence tolerance: 1.785e-07
> confint(result) # 95% confidence interval
Waiting for profiling to be done...
2.5% 97.5%
Rt 3.148358 3.652665
Kd 15.470323 21.906326
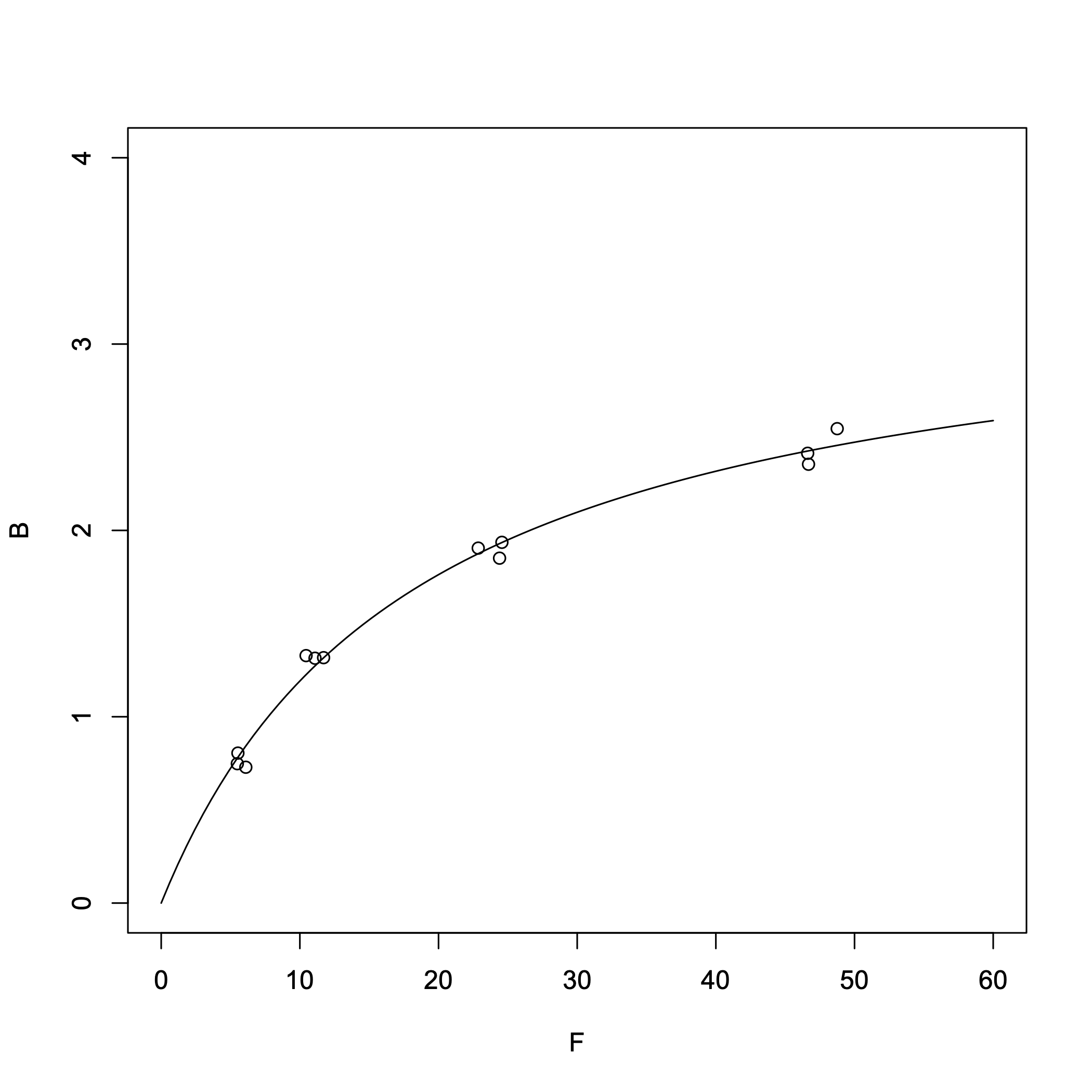
From the nonlinear regression, we obtained:
- Dissociation constant \(K_{\rm d}\) = 18.4 nM
- \([R_{\rm T}]\) = 3.38 nM
> result_lm = lm(B/F ~ B) > summary(result_lm)Output:
Call:
lm(formula = B/F ~ B)
Residuals:
Min 1Q Median 3Q Max
-0.0207551 -0.0043123 0.0007946 0.0048720 0.0171733
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.177090 0.008028 22.06 8.21e-10 ***
B -0.050571 0.004659 -10.85 7.46e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01015 on 10 degrees of freedom
Multiple R-squared: 0.9218, Adjusted R-squared: 0.9139
F-statistic: 117.8 on 1 and 10 DF, p-value: 7.464e-07
> confint(result_lm)
2.5 % 97.5 %
(Intercept) 0.15920357 0.1949766
B -0.06095189 -0.0401892
> -1/result_lm$coefficients[2]
B
19.77436
> -result_lm$coefficients[1]/result_lm$coefficients[2]
(Intercept)
3.501842
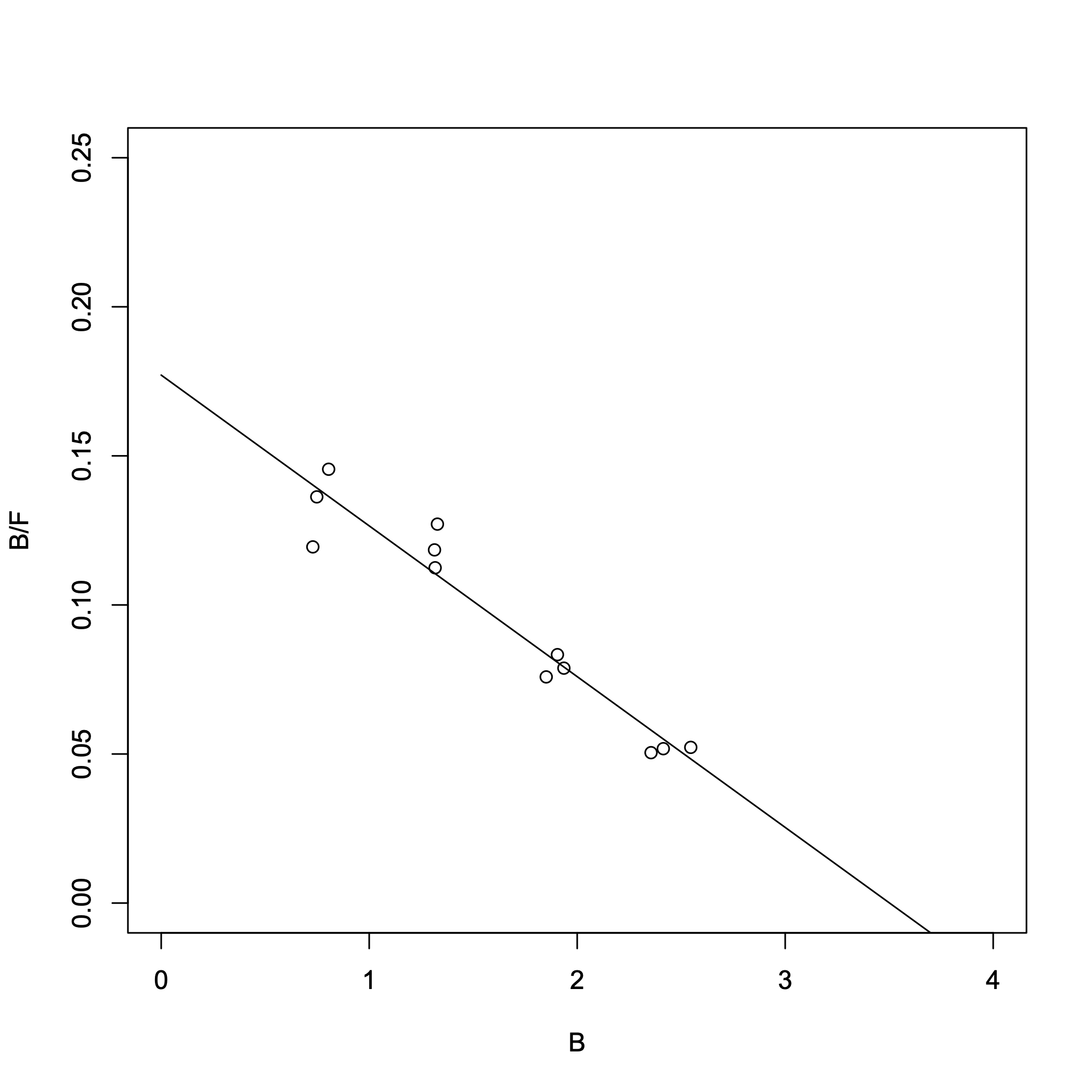
The two lowest-concentration B/F values overlap in range. (Because the inverse of F is used, the error becomes significantly amplified.) From the Scatchard plot, we obtained:
- Dissociation constant \(K_{\rm d}\) = 19.8 nM
- \([R_{\rm T}]\) = 3.50 nM
Comparing the 95% confidence intervals for \(K_{\rm d}\):
- Nonlinear regression: \(K_{\rm d}\) = 18.4 nM (95% CI: 15.5–21.9)
- Scatchard plot: \(K_{\rm d}\) = 19.8 nM (95% CI: 16.4–24.9)
References
- Braun, Derek C.; Garfield, Susan H.; Blumberg, Peter M. “Analysis by Fluorescence Resonance Energy Transfer of the Interaction between Ligands and Protein Kinase Cδ in the Intact Cell”. J. Biol. Chem. 2005, 280(9), 8164-8171. doi: 10.1074/jbc.M413896200
- Scatchard, George “The Attraction of Proteins for Small Molecules and Ions”. Annals of the New York Academy of Sciences 1949, 51(4), 660–672. doi: 10.1111/j.1749-6632.1949.tb27297.x.