(2025年6月24日更新)
Contents
テキストを読んでいて気になったこと
実験テキストを見ていたら、少し気になる記述があって調べ物をしたのでメモ。井口豊(2025-02-17)等分散検定から t検定,ウェルチ検定,U検定への問題点が大変参考になりました。テキストでは教育的に正規性の検定(Shapiro–Wilk検定)、等分散性の検定(F検定)、分散分析、t検定、Welchのt検定、ノンパラメトリック法(Wilcoxonの符号付き順位検定、Kruskal–Wallis検定)、そして第一種の過誤を制御する方法としてBonferroniの方法が説明されています。教育的でよいのですが、1) 検定の多重性の問題(例えばF検定→t検定という手順)、2) 分散分析→多重比較という手順、3) ノンパラメトリック検定について、4) 正規性の検定の必要性、の4点が気になりました。講義や実習中ではきちんと説明されているかもしれませんが。
その1) 検定の多重性の問題
等分散性の検定(2群の場合はF検定、3群以上では分散分析(ANOVA))→F検定の結果を受けてWelchの補正を加えるか決定する、という手順が書かれています。これは以下の理由でよくないです。
- F検定とt検定をそれぞれある有意水準(例えば5%)で行った場合、検定全体の第一種の過誤を(5%以内に)制御できない検定の多重性の問題が生じる。
等分散であるかどうかを確かめてから,普通の t 検定を使うか,Welch の方法による t 検定にするかを決めるというのは,よくない。最初から Welch の方法による t 検定を使えばよい。(青木繁伸(2007-02-08)二群の等分散性の検定; 井口豊(2025-02-17)等分散検定から t検定,ウェルチ検定,U検定への問題点)
総じて、Welchのt検定を使うことで誤った判断を下す確率が減るため、基本的には等分散性の仮定が成り立つかに関わらずWelchのt検定の使用が推奨されている。Rのデフォルトのt検定もWelchのt検定である。(野村康之、t検定の再考1: 等分散性)
この検定の多重性の問題ですが、例えば同じ確率分布に従う2つの群について、F検定とt検定をそれぞれ有意水準5%で連続して行ったとします。この場合の帰無仮説が正しいにもかかわらずそれを誤って棄却してしまう確率(第一種の過誤、αエラー)を計算します。両検定とも正しく帰無仮説を採択する確率は\(0.95 \times 0.95 = 0.95^2\)です。両方もしくは片方の検定で誤って帰無仮説を棄却する確率は\(1 – 0.95^2 = 0.0975\)となります。元々は第一種の過誤を5%以内に抑えたかったのに、検定全体としては9.75%と10%近い値になってしまうのが検定の多重性の問題です。
その2) 分散分析→多重比較という手順
基本的に多重比較検定よりも分散分析の方が検出力が高いので、この手順に実用上問題はほとんどないと思います。しかし、分散分析で有意差がなくても、群間多重比較で有意となる場合が(ごく稀に)あります(vice versa、分散分析で有意にならないが、多重比較検定で有意となるようなデータの例)。A、B、Cの3つの群を比較する場合を考えると、分散分析の帰無仮説はすべての群の母平均(\(\mu_A, \mu_B, \mu_C\))が等しい(\(\mu_A = \mu_B = \mu_C\))なのに対して、多重比較(例えばTukeyのHSD検定)の帰無仮説族(ファミリー)は\(\mu_A = \mu_B, \mu_B = \mu_C, \mu_A= \mu_C\)であり異なっているためです。
多重比較法の中でScheffeの方法、Fisherの制約付きLSD法 (Fisher’s Protected Least Significant Difference) はF分布を使用するので、手順に分散分析が組込まれています。分散分析で有意差が出なければ、これらの方法でも有意差は出ません。その他の多重比較法(TukeyのHSD法、Games–Howell法、Dunnettの方法、DunnettのC法、Welchのt検定のBonferroni補正、Welchのt検定のHolm–Bonferroni補正など)はF分布を使用しないので分散分析を事前に行わないのが原則です(つまりこれらは分散分析のpost-hoc(事後)解析法ではない)。
一言で答えると、「用いる多重比較法の手順の中に含まれている場合のみ一元配置分散分析を行う」となる。それ以外の場合には、分散分析は不要なのではなく、行わないことが原則である。(永田靖. 多重比較法の実際 応用統計学、1998 年 27 巻 2 号 p. 93-108)
その3) ノンパラメトリックな検定についての注意点
標本(群)に母集団が正規分布に従わないものがある場合は、Wilcoxonの順位和検定(Mann–WhitneyのU検定と等価)やKruskal–Wallis検定といったノンパラメトリックな検定を行う旨が書かれています。これは危険です。
Mann–WhitneyのU検定(Wilcoxonの順位和検定)の帰無仮説は「2つの標本の順位の平均が等しい = 2つの標本の母集団の分布が同じ」です。「2つの標本の母集団の平均や中央値が等しい」ではありません。2つの標本は同じ確率分布からサンプリングされていることが想定されます。対立仮説は「2つの標本の順位の平均は異なる ≒ ある群からの観測値が、もう一方の群からの観測値より大きくなる」となります。そもそも平均値や中央値の差を検定したい時にはMann–WhitneyのU検定を使うべきではないということです。平均値の検定にはWelchのt検定を、中央値の等しさを検定したい場合は分位点回帰を使用するべきです。問題のややこしさは、2つの集団の分布形状が同一である場合にMann–WhitneyのU検定を「中央値の等しさの検定」と解釈できてしまう点にあります。しかし実際のデータでは、分布形状が同一で位置がシフトしているだけと仮定できることはほとんどないと思います。後で不等分散の場合にどうなるかシミュレーションしていますが、不等分散の場合は群間の違いについて検定結果から解釈することができません(参考: 粕谷英一(2001-11-04)Mann–WhitneyのU検定と不等分散のページ)。Googleで検索すると、ノンパラメトリック検定が正規性も等分散性も必要としない、との誤解が書かれている(もしくはそのように読める)記事もちらほらあります。また、「等分散性を必要とする」というのも間違いで、分散については何の仮定も置かれません。
非正規分布、非等分散のデータにて適用できるノンパラメトリック検定としてはBrunner–Munzel検定が推奨されています(井口豊(2025-02-17)等分散検定から t検定,ウェルチ検定,U検定への問題点)。Brunner–Munzel検定の帰無仮説は「2群から1個ずつ取り出したとき、ある群からの値が別の群の値よりも大きくなる確率と同じになる確率の半分の合算が1/2になる」ことで、対立仮説は「どちらかの群が全体的に大きな値を持つ」です(名取真人. マン・ホイットニーのU検定と不等分散時における代表値の検定法 霊長類研究、2014 年 30 巻 1 号 p. 173-185)。
対してt検定による2群比較の帰無仮説は「一つ目の母集団の平均値μ1が2つ目の母集団の平均値μ2と等しい」です。「平均値の差の検定」であり「中心極限定理」が効いてくるため、t検定は正規分布してないデータに対しても頑健(robust)であると言われています。ただし、正規母集団に対してはn = 2でも大丈夫なのに対して、「指数母集団の場合は,適切な結果を得るには,標本サイズが100以上必要」(井口豊(2022-12-06)小標本 t 検定の誤解:中心極限定理と一般化線形モデル)。
正規性も等分散性も成り立たない状況では、平均値の比較ならWelchのt検定、中央値の比較ならBrunner-Munzel検定が検定精度がよい傾向にある。(冨田 哲治、Brunner-Munzel検定)
Welchのt検定は非正規性に対しても非等分散性に対しても頑健なのに対して、Wilcoxonの順位和検定などは脆弱な方法であると言われます。
その4) 正規性の検定の結果を受けてt検定かノンパラメトリックな検定かを選択する問題点
「標本(群)ごとにShapiro–Wilk検定をおこなって各標本(群)の母集団が正規分布に従うかを検定」して、t検定かノンパラメトリックな検定かを選択する旨が書かれていました。
Shapiro–Wilk検定を事前に行うことも「多重性の問題」と「サンプルサイズで検定結果は左右」されるため、推奨されていません。
群ごとや,要因の水準ごとに正規性を検定すると,何が問題なのか?ごく簡単なことで,検定の多重性が問題になるのである。(井口豊(2022-09-12)分散分析の正規性は残差を調べる:検定の多重性問題)
ではどうやって正規性を判断するかというと
基本的には、ヒストグラムを描いて釣り鐘状になっているかを観察します。経験的知見から「このデータは正規分布に従うはずだ」と思えば、正規分布として解析してもかまいません。(「いちばんやさしい、医療統計」(2024-05-07)SPSSで正規性の検定(シャピロウィルクやKolmogorov-Smirnov)を実施する方法!)
用語のおさらい
- 正規分布(せいきぶんぷ)— ガウス関数\(f(x) = e^{-x^2}\)の分布。平均\(\mu\)、分散\(\sigma^2 > 0\)の正規分布は、$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$$
- 大数の法則(たいすうのほうそく) — 標本数を増やしていけば同一な分布から生成した確率変数の算術平均(標本平均)が、母集団の平均(期待値)が存在するならば、この母平均に収束する、という主張。
- 中心極限定理(ちゅうしんきょくげんていり)— 母集団の確率分布が有限の分散を持つならば、どのような形のの確率分布を持つ母集団から取られた標本でも、その標本平均の確率分布は正規分布になる、という定理。
- t検定(ティーけんてい)— 大雑把に言うと、2つの群の平均値の差を全体の標準誤差で割った値を検定統計量t $$t_0 = \frac{|\bar{X} – \bar{Y}|}{\sqrt{U_e\left(\frac{1}{m}+\frac{1}{n}\right)}}$$ として、平均値が同じ場合(帰無仮説)にこのtが従う分布、t分布を元にして得られた検定統計量がどれほど起こりづらいか、を判断する。
見ておくべき動画
KyotoU Channel(2018-01-11)臨床研究者のための生物統計学「仮説検定とP値の誤解」佐藤俊哉(医学研究科教授)
統計モデルは一連の仮定(ランダム化・ランダムサンプリングがなされている、研究計画が遵守されている、すべての解析結果が報告されている、など)で構成されている。帰無仮説はその仮定の一つに過ぎない。P値が小さいことは「たくさんある統計モデルに必要な仮定のうちどれか1つあるいは複数が間違っている」ことを意味する。決して帰無仮説だけが間違いの対象ではない。
Rを使ったシミュレーション
参考サイト: 井口豊(2022-12-06)小標本 t 検定の誤解:中心極限定理と一般化線形モデル
R 4.5.1 (macOS) を使用。比較する2群は全て標本サイズ (n) が同じ。
先に自分なりの結論(教訓、反省):
- n = 2や3でどうのこうのいうのは危ない。
- ノンパラメトリックな方法として代表的なMann–WhitneyのU検定(Wilcoxonの順位和検定)は平均値や中央値に差があるかを検定する方法ではないため、そのような用途で使用すべきではない。
- Welchのt検定は確かに頑健。
母集団が正規分布の場合(等分散)

Studentのt検定
k <- 100000 # 標本取り出し反復回数
n <- 4 # 標本サイズ
r <- replicate(k, {
x <- rnorm(n, mean=0, sd=1)
y <- rnorm(n, mean=0, sd=1)
c(mean(x), t.test(x, y, var.equal=TRUE)$p.value)
})
m <- r[1, ] # 平均値
p <- r[2, ] # 5%水準棄却数
reject_rate <- length(p[p<=0.05])/k # 5%水準棄却率
print (reject_rate)
[1] 0.04981
Welchのt検定
k <- 100000 # 標本取り出し反復回数
n <- 4 # 標本サイズ
r <- replicate(k, {
x <- rnorm(n, mean=0, sd=1)
y <- rnorm(n, mean=0, sd=1)
c(mean(x), t.test(x, y, var.equal=FALSE)$p.value)
})
m <- r[1, ] # 平均値
p <- r[2, ] # 5%水準棄却数
reject_rate <- length(p[p<=0.05])/k # 5%水準棄却率
print (reject_rate)
[1] 0.0413
Mann–WhitneyのU検定
k <- 100000 # 標本取り出し反復回数
n <- 4 # 標本サイズ
r <- replicate(k,{
x <- rnorm(n, mean=0, sd=1) #平均0、標準偏差1の正規分布からランダムサンプリング
y <- rnorm(n, mean=0, sd=1)
c(mean(x), wilcox.test(x, y)$p.value)
})
m <- r[1, ] # 平均値
p <- r[2, ] # 5%水準棄却数
reject_rate <- length(p[p<=0.05])/k # 5%水準棄却率
print (reject_rate)
[1] 0.02919
結果
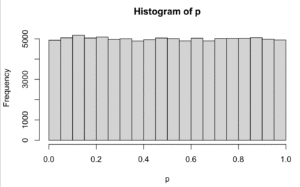
同一の確率分布からn個の標本を2回取り出して2つの群に差があるかを検定する (p値を計算する)、を10万回繰り返してp ≦ 0.05となった確率。
| 5%水準棄却率 | |||
| n | Studentのt検定 | Welchのt検定 | Mann–WhitneyのU検定 |
| 2 | 0.05012 | 0.02321 | – |
| 3 | 0.05059 | 0.03456 | – |
| 4 | 0.04981 | 0.0413 | 0.02919 |
| 5 | 0.04999 | 0.04404 | 0.03144 |
| 6 | 0.5104 | 0.04493 | 0.04067 |
| 7 | 0.04942 | 0.0475 | 0.03808 |
| 8 | 0.04975 | 0.04699 | 0.05012 |
| 9 | 0.04983 | 0.04841 | 0.03832 |
| 10 | 0.5097 | 0.04846 | 0.04357 |
| 20 | 0.04845 | 0.05003 | 0.04874 |
| 30 | 0.05017 | 0.04939 | 0.05059 |
| 40 | 0.04979 | 0.04889 | 0.05027 |
| 50 | 0.04945 | 0.05065 | 0.04892 |
| 60 | 0.04934 | 0.04954 | 0.05057 |
| 70 | 0.0502 | 0.0482 | 0.05015 |
| 80 | 0.05082 | 0.05107 | 0.05006 |
| 90 | 0.05024 | 0.04976 | 0.05034 |
| 100 | 0.04899 | 0.04974 | 0.04987 |
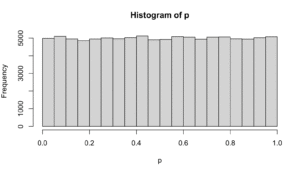
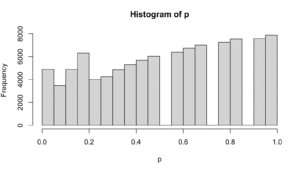
モデル通りなのでStudentのt検定はn = 2でも正確です。Welchのt検定はn数が少ない時は棄却率が低いです。同じ分布の比較なのでMann–WhitneyのU検定も中央値の検定として振る舞っています。
母集団が正規分布で分散が異なる場合
標本サイズが等しい場合
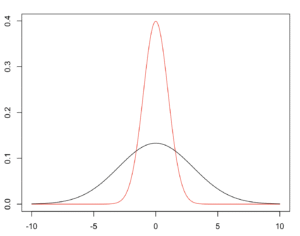
正規分布A(平均0、標準偏差=1、赤)vs. 正規分布B(平均値=0、標準偏差=3、黒)。
| 5%水準棄却率 | |||
| n | Studentのt検定 | Welchのt検定 | Mann–WhitneyのU検定 |
| 2 | 0.07343 | 0.03688 | – |
| 3 | 0.07413 | 0.05227 | – |
| 4 | 0.07121 | 0.05398 | 0.04841 |
| 5 | 0.06767 | 0.05187 | 0.04509 |
| 6 | 0.06437 | 0.05248 | 0.0494 |
| 7 | 0.06227 | 0.05126 | 0.054 |
| 8 | 0.06005 | 0.0508 | 0.0671 |
| 9 | 0.0599 | 0.05179 | 0.05365 |
| 10 | 0.06025 | 0.05017 | 0.0605 |
| 20 | 0.05343 | 0.05068 | 0.06728 |
| 30 | 0.05162 | 0.05059 | 0.06818 |
| 40 | 0.05231 | 0.05047 | 0.06974 |
| 50 | 0.05168 | 0.05018 | 0.06915 |
| 60 | 0.05254 | 0.04984 | 0.06906 |
| 70 | 0.05084 | 0.05022 | 0.0694 |
| 80 | 0.04975 | 0.04894 | 0.06913 |
| 90 | 0.0505 | 0.05116 | 0.06784 |
| 100 | 0.0503 | 0.05021 | 0.06722 |
Welchのt検定は理論通り不等分散の場合でも大丈夫でした。Studentのt検定はnが大きければ正しく振る舞っています。これはなぜかといえば標本サイズ(n)が等しいからです。生物系の実験の場合はn数を揃えるのが普通なのであまり意識されませんが、これはかなり大事です。nが十分大きく、nを揃えていれば、Studentのt検定やTukeyのHSD検定は不等分散に対して頑健です。逆に言うとn数が異なる場合は等分散性に注意を払う必要があります。
大事なことですが、nが揃っていればStudentのt検定とWelchのt検定の統計量tは等しいです。統計量tの計算式を下に示します。
Studentのt検定の統計量t(\(m\)と\(n\)は標本サイズ、\(\bar{X}\)と\(\bar{Y}\)は標本平均、\(U_x\)と\(U_y\)は不偏分散)
$$t_0 = \frac{|\bar{X} - \bar{Y}|}{\sqrt{U_e\left(\frac{1}{m}+\frac{1}{n}\right)}} $$ $$U_e = \frac{(m-1)U_x + (n-1)U_y}{m+n-2} $$ 両群の母平均が等しい場合には「統計量\(t_0\)は自由度\(\nu = m+n-2\)のt分布に従う」。
Welchのt検定の統計量t:
$$t_0 = \frac{|\bar{X} - \bar{Y}|}{\sqrt{\frac{U_x}{m}+\frac{U_y}{n}}} $$ 両群の母平均が等しい場合には「統計量\(t_0\)は自由度 $$\nu \simeq \frac{\left(\frac{U_x}{m} + \frac{U_y}{n}\right)^2}{\frac{U_x^2}{m^2(m-1)}+\frac{U_y^2}{n^2(n-1)}}$$ のt分布に従う」。
\(m = n\) の時は、Studentのt検定の自由度:$$ \nu_{Student} = 2(m-1)$$
Welchのt検定の自由度:$$ \nu_{Welch} = \left(1+\frac{2U_x U_y}{U_x^2 + U_y^2}\right)(m-1)$$
です。\(U_x = U_y\) ならば両検定の自由度も等しくなります。
標本サイズが異なる場合
次に片方(標準偏差が大きい方)のnを2倍にして同様に5%水準棄却率がどうなるか試してみます。
| 5%水準棄却率 | ||||
| nA | nB | Studentのt検定 | Welchのt検定 | Mann–WhitneyのU検定 |
| 2 | 4 | 0.02764 | 0.03732 | – |
| 3 | 6 | 0.02481 | 0.04337 | 0.02842 |
| 4 | 8 | 0.02256 | 0.04636 | 0.03206 |
| 5 | 10 | 0.02192 | 0.04828 | 0.02558 |
| 6 | 12 | 0.02114 | 0.04861 | 0.02713 |
| 7 | 14 | 0.01966 | 0.04846 | 0.02961 |
| 8 | 16 | 0.01961 | 0.04942 | 0.02801 |
| 9 | 18 | 0.01904 | 0.04894 | 0.02933 |
| 10 | 20 | 0.01779 | 0.04861 | 0.03106 |
| 20 | 40 | 0.01712 | 0.0498 | 0.03161 |
| 30 | 60 | 0.0172 | 0.05002 | 0.03247 |
| 40 | 80 | 0.01693 | 0.05006 | 0.03308 |
| 50 | 100 | 0.01711 | 0.04997 | 0.03287 |
| 60 | 120 | 0.01738 | 0.05036 | 0.03274 |
| 70 | 140 | 0.01668 | 0.05035 | 0.03205 |
| 80 | 160 | 0.01672 | 0.04971 | 0.03289 |
| 90 | 180 | 0.01651 | 0.05049 | 0.03343 |
| 100 | 200 | 0.01684 | 0.05071 | 0.03394 |
Welchのt検定だけが第一種の過誤を制御できていました。
母集団が正規分布でない場合(二峰分布)(等分散)
ピークが2つあるフタコブラクダのような分布(二峰分布)を考えます(参考: 備忘録 a record of inner life(2015-02-23)Rでの分布作成と自作分布に従う乱数生成)。
fx <- function(x) dnorm(x, mean=2, sd=1) gx <- function(x) dnorm(x, mean=-2, sd=2) hx <- function(x) 1/2*(fx(x)+gx(x)) plot(hx, xlim=c(-10, 10))
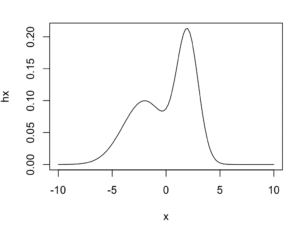
$$h(x) = \frac{1}{2}\left(\frac{1}{\sqrt{2\pi 1^2}}\exp\left(-\frac{(x-2)^2}{2\times 1^2}\right) + \frac{1}{\sqrt{2\pi 2^2}}\exp\left(-\frac{(x+2)^2}{2\times 2^2}\right)\right)\;\;\;(-10 < x < 10)$$という分布に従う乱数を生成します。
rbimodal <- function(x, m1=2, s1=1, m2=-2, s2=2) {
u <- rbinom(x, 1, 0.5)
v <- sum(u == 0)
w <- x - v
y <- c(rnorm(v, mean=m1, sd=s1), rnorm(w, mean=m2, sd=s2))
return(y)
}
結果(二峰分布)
| 5%水準棄却率 | |||
| n | Studentのt検定 | Welchのt検定 | Mann–WhitneyのU検定 |
| 2 | 0.06412 | 0.03159 | – |
| 3 | 0.05416 | 0.0378 | – |
| 4 | 0.05186 | 0.0386 | 0.02903 |
| 5 | 0.05066 | 0.04235 | 0.3167 |
| 6 | 0.05317 | 0.04427 | 0.04131 |
| 7 | 0.05143 | 0.04655 | 0.03748 |
| 8 | 0.05117 | 0.04831 | 0.0502 |
| 9 | 0.05075 | 0.04865 | 0.03999 |
| 10 | 0.05224 | 0.04889 | 0.04317 |
| 20 | 0.05087 | 0.04944 | 0.0492 |
| 30 | 0.04999 | 0.04898 | 0.05071 |
| 40 | 0.05004 | 0.04958 | 0.04987 |
| 50 | 0.04907 | 0.05007 | 0.04913 |
| 60 | 0.04973 | 0.05102 | 0.04896 |
| 70 | 0.0507 | 0.04947 | 0.04822 |
| 80 | 0.05108 | 0.0495 | 0.04966 |
| 90 | 0.05016 | 0.04983 | 0.04975 |
| 100 | 0.05063 | 0.04968 | 0.04878 |
正規分布でなくてもt検定は使えることが分かります。
母集団の片方が正規分布でない場合(二峰分布)
以下のような正規分布(赤)と二峰分布(黒)から取出した標本同士を比べます。
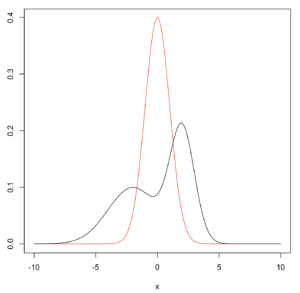
※注意書き
このような標本が取れたときに、まず考えてほしいのはこれらの標本は本当に比較するべきか、ということである。特に二峰分布のほうは、もしかしたら分けられるべき標本が混じっている可能性も考えるべきである。なにも考えずにただ検定するのは良い手とは言えない。(野村康之. Brunner-Munzel検定)
| 5%水準棄却率 | |||
| n | Studentのt検定 | Welchのt検定 | Mann–WhitneyのU検定 |
| 2 | 0.09888 | 0.04859 | – |
| 3 | 0.10786 | 0.08199 | – |
| 4 | 0.09623 | 0.08372 | 0.06325 |
| 5 | 0.0827 | 0.07315 | 0.05605 |
| 6 | 0.07439 | 0.06804 | 0.0574 |
| 7 | 0.0723 | 0.06359 | 0.07345 |
| 8 | 0.06735 | 0.06174 | 0.08358 |
| 9 | 0.06505 | 0.05893 | 0.07089 |
| 10 | 0.06399 | 0.05903 | 0.08386 |
| 20 | 0.05663 | 0.05369 | 0.1107 |
| 30 | 0.05363 | 0.0525 | 0.13456 |
| 40 | 0.05371 | 0.05193 | 0.15399 |
| 50 | 0.05201 | 0.05032 | 0.17493 |
| 60 | 0.05266 | 0.05315 | 0.19635 |
| 70 | 0.05169 | 0.04962 | 0.21546 |
| 80 | 0.05188 | 0.05155 | 0.23806 |
| 90 | 0.05183 | 0.04997 | 0.25626 |
| 100 | 0.0522 | 0.05032 | 0.27582 |
n ≧ 50でWelchのt検定はよい結果。
母集団の片方が正規分布でない場合(コーシー分布)
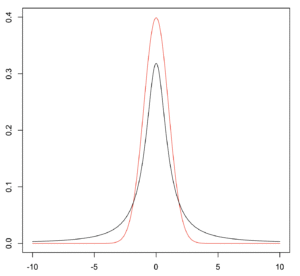
正規分布 (赤) vs. コーシー分布(黒)。コーシー分布は以下のような裾が重い関数です。
$$ f(x;x_0,\gamma) = \frac{1}{\pi}\frac{\gamma}{(x-x_0)^2 + \gamma^2} $$
裾が重く、期待値(平均)と分散が定義されません(\(x_0\)は最頻値、\(\gamma\)は半値半幅を与える値)。そのため、大数の法則と中心極限定理が成立しません。関数形はローレンツ関数とも呼ばれる形で、フーリエ変換NMRの勉強をしている時に片側指数関数のフーリエ変換が複素ローレンツ関数となる(つまりNMRピークの形状はローレンツ関数ということ)ので馴染があるかと思います。
| 5%水準棄却率 | ||||
| n | Studentのt検定 | Welchのt検定 | Mann–WhitneyのU検定 | Brunner–Munzel検定 |
| 2 | 0.03864 | 0.0178 | – | 0.034374 |
| 3 | 0.03061 | 0.01983 | – | 0.10554 |
| 4 | 0.02931 | 0.0208 | 0.3132 | 0.06119 |
| 5 | 0.02926 | 0.02222 | 0.03513 | 0.08471 |
| 6 | 0.02839 | 0.02215 | 0.04258 | 0.06577 |
| 7 | 0.02742 | 0.2202 | 0.03998 | 0.05692 |
| 8 | 0.02784 | 0.02232 | 0.05294 | 0.05751 |
| 9 | 0.0277 | 0.0225 | 0.04167 | 0.05662 |
| 10 | 0.02598 | 0.02123 | 0.04524 | 0.0542 |
| 20 | 0.02532 | 0.0221 | 0.05336 | 0.05326 |
| 30 | 0.02341 | 0.02129 | 0.05273 | 0.05124 |
| 40 | 0.02425 | 0.02222 | 0.05483 | 0.05229 |
| 50 | 0.02291 | 0.02155 | 0.05373 | 0.05132 |
| 60 | 0.02309 | 0.02169 | 0.05439 | 0.05169 |
| 70 | 0.02168 | 0.0206 | 0.05398 | 0.05109 |
| 80 | 0.02199 | 0.0209 | 0.05407 | 0.05177 |
| 90 | 0.02217 | 0.02134 | 0.05409 | 0.05088 |
| 100 | 0.02186 | 0.02106 | 0.05457 | 0.05151 |
母集団が正規分布でない場合: 二峰分布 vs. コーシー分布
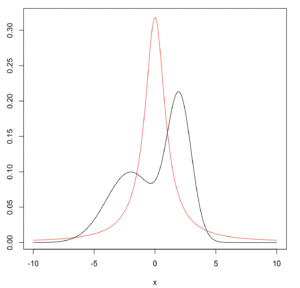
コーシー分布(赤)vs. 二峰分布(黒)。
x <- seq(-10,10,by=0.1) plot(dcauchy, -10, 10, n=1001, col='red') #コーシー分布(赤) lines(x, hx(x),col="black") #フタコブ分布(黒)
k <- 100000
N = c(2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100)
for (n in N){
r <- replicate(k, {
x <- rbimodal(n)
y <- rcauchy(n) # コーシー分布に従う乱数発生
c(t.test(x, y, var.equal=TRUE)$p.value,
t.test(x, y, var.equal=FALSE)$p.value,
wilcox.test(x, y)$p.value)
})
p_1 <- r[1, ]
p_2 <- r[2, ]
p_3 <- r[3, ]
reject_1 <- length(p_1[p_1<=0.05])/k # 5%水準棄却率
reject_2 <- length(p_2[p_2<=0.05])/k
reject_3 <- length(p_3[p_3<=0.05])/k
cat(n, format(reject_1, 5), format(reject_2, 5), format(reject_3, 5), "\n")
}
結果(二峰分布とコーシー分布)
| 5%水準棄却率 | |||
| n | Studentのt検定 | Welchのt検定 | Mann–WhitneyのU検定 |
| 2 | 0.06123 | 0.03007 | – |
| 3 | 0.05921 | 0.04252 | – |
| 4 | 0.049 | 0.03999 | 0.04217 |
| 5 | 0.04399 | 0.03709 | 0.03969 |
| 6 | 0.03881 | 0.03345 | 0.05023 |
| 7 | 0.03627 | 0.03327 | 0.04951 |
| 8 | 0.03615 | 0.03138 | 0.06096 |
| 9 | 0.03367 | 0.03047 | 0.05204 |
| 10 | 0.03342 | 0.02977 | 0.05697 |
| 20 | 0.02933 | 0.02661 | 0.07293 |
| 30 | 0.02776 | 0.02695 | 0.08275 |
| 40 | 0.02662 | 0.02555 | 0.09228 |
| 50 | 0.02531 | 0.02464 | 0.10031 |
| 60 | 0.02519 | 0.02456 | 0.10849 |
| 70 | 0.02444 | 0.02405 | 0.11873 |
| 80 | 0.02441 | 0.02401 | 0.12666 |
| 90 | 0.02444 | 0.02302 | 0.13748 |
| 100 | 0.02375 | 0.02377 | 0.14521 |
母集団が正規分布で平均値と分散が異なる場合
正規分布(平均=1、標準偏差=2、赤)vs. 正規分布(平均値=-1、標準偏差=4、黒)。効果量(平均の差÷標準偏差)は$$\frac{|1-(-1)|}{\sqrt{\frac{2^2+4^2}{2}}} \fallingdotseq 0.632$$で中程度と言えます(d = 0.2(小さい効果)、0.5(中程度の効果)、0.8(大きい効果))。
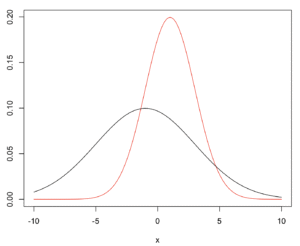
| 5%水準棄却率 | |||
| n | Studentのt検定 | Welchのt検定 | Mann–WhitneyのU検定 |
| 2 | 0.08122 | 0.03849 | – |
| 3 | 0.10877 | 0.07941 | – |
| 4 | 0.13293 | 0.10722 | 0.08771 |
| 5 | 0.15622 | 0.13357 | 0.10983 |
| 6 | 0.17949 | 0.16056 | 0.14395 |
| 7 | 0.20341 | 0.18465 | 0.16496 |
| 8 | 0.22851 | 0.20847 | 0.21961 |
| 9 | 0.25064 | 0.23274 | 0.2131 |
| 10 | 0.27669 | 0.25696 | 0.24706 |
| 20 | 0.499 | 0.48885 | 0.47347 |
| 30 | 0.6711 | 0.66596 | 0.64369 |
| 40 | 0.79825 | 0.79321 | 0.76642 |
| 50 | 0.87752 | 0.87767 | 0.85248 |
| 60 | 0.9303 | 0.927 | 0.9094 |
| 70 | 0.95973 | 0.95921 | 0.94547 |
| 80 | 0.97866 | 0.97803 | 0.96824 |
| 90 | 0.9882 | 0.98743 | 0.98103 |
| 100 | 0.99358 | 0.99353 | 0.98912 |
参考文献
1) 永田靖・吉田道弘(1997).統計的多重比較法の基礎 サイエンティスト社