先日の文献セミナーで酵素阻害剤の阻害様式とIC50とKiの関係についてよく分かっていなくて、頓珍漢な質問をしてしまったのでメモ。
Contents
まとめ(引用)
まず結論を引用します。
IC50とKi値の関係は、in vitroの試験では [S] >> Kmが成立するので、非拮抗阻害や不拮抗阻害ではIC50 = Kiであり、拮抗阻害ではKi = IC50/(1 + [S]/Km) からKi値が換算される(Km: ミカエリス定数、Ki: 阻害定数)
— 安達ら、2010
解説
各阻害様式の定義(純粋型)
- (純粋な)拮抗阻害(competitive inhibition; 競合阻害/競争阻害)では、阻害剤 I は E にのみ結合する。
- 非拮抗阻害(non-competitive inhibition; 非競合阻害/非競争阻害)では、阻害剤 I は E にも ES にも同じ親和性で結合する。
- (純粋な)不拮抗阻害(uncompetitive inhibition; 不競合阻害/不競争阻害)では、阻害剤 I は ES にのみ結合する。

IC50とKiの一般式
50%阻害濃度IC50と阻害定数Kiの関係は以下の近似式(式1)で表わされます。
\[ {\mathrm{IC}}_{50} = \frac{[S]_0 + K_{\mathrm m}}{\frac{K_{\mathrm m}}{K_{\mathrm i}} + \frac{[S]_0}{\alpha K_{\mathrm i}}} \;\;\;\mbox{・・・式1}\]
式1において、\([S]_0\) は基質の初期濃度を表わします: \([S]_0 = [S] + [ES] + [ESI] + [P] \)。
この式は混合型阻害(mixed-type inhibition; Ki ≠ αKi)に対するCheng–Prusoff式(Cheng and Prusoff, 1973のCase II)と同一です。阻害様式を解析する目的で、IC50を [S]0/Kmに対してプロットしたいので、式1を変形すると次のようになります。 $$ {\mathrm{IC}}_{50} = \frac{1 + \frac{[S]_0}{K_{\mathrm m}}}{\frac{1}{K_{\mathrm i}} + \left(\frac{1}{\alpha K_{\mathrm i}} \times \frac{[S]_0}{K_{\mathrm m}}\right)} $$
各阻害様式での極限
拮抗阻害(\(\alpha\to \infty\))
$$ {\mathrm{IC}}_{50} = \frac{1 + \frac{[S]}{K_{\mathrm m}}}{\frac{1}{K_{\mathrm i}}} = K_{\mathrm i} \left(1 + \frac{[S]}{K_{\mathrm m}}\right)$$
非拮抗阻害(\(\alpha = 1\))
$$ {\mathrm{IC}}_{50} = K_{\mathrm i}$$
不拮抗阻害(\(K_{\mathrm i}\to \infty\)、ただし\( \alpha K_{\mathrm i}\) が有限の場合)
$$ {\mathrm{IC}}_{50} = \alpha K_{\mathrm i} \left(1 + \frac{K_{\mathrm m}}{[S]}\right)$$
特に\([S] \gg K_{\mathrm m}\)の条件下では、
$$ \mathrm{IC}_{50} \sim \alpha K_{\mathrm i} $$
まとめの表:
| 阻害機構 | パラメータ | IC50 |
|---|---|---|
| 拮抗(competitive) | \(\alpha\to \infty \) | \( K_{\mathrm i} \left(1 + \frac{[S]}{K_{\mathrm m}}\right)\) |
| 非拮抗(non-competitive) | \( \alpha = 1 \) | \( K_{\mathrm i}\) |
| 不拮抗(uncompetitive) | \(K_{\mathrm i}\to \infty\)、\( \alpha K_{\mathrm i} \ll K_{\mathrm i}\) | \( \alpha K_{\mathrm i} \left(1 + \frac{K_{\mathrm m}}{[S]}\right)\) |
| 混合(mixed) | – | \( \frac{[S] + K_{\mathrm m}}{\frac{K_{\mathrm m}}{K_{\mathrm i}} + \frac{[S]}{\alpha K_{\mathrm i}}} \) |
それぞれの阻害様式について、 [S]/Kmに対してIC50をプロットしたものが以下の図です。

セミナーで紹介された論文ではこのプロットが “Cheng–Prusoff plot” と呼ばれていました。
式1の導出
導出はCheng and Prusoff, 1973のCase IIから。
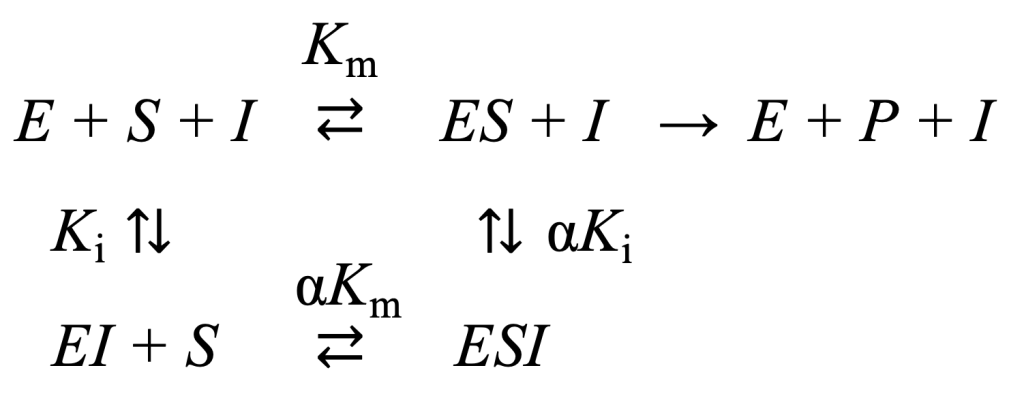
反応系は迅速に平衡に達すると仮定します。したがって、\(k_{-1} \gg k_{cat} \) なので、\(K_{\mathrm{s}} = K_{\mathrm{m}} + \frac{k_{cat}}{k_{-1}} \sim K_{\mathrm{m}} \) が成り立ちます。
定義式
$$ K_{\mathrm{m}} \sim K_{\mathrm{s}} = \frac{[E][S]}{[ES]} \;\;\;\mbox{・・・式2}$$
$$ K_{\mathrm{i}} = \frac{[E][I]}{[EI]} \;\;\;\mbox{・・・式3}$$
$$ \alpha K_{\mathrm{i}} = \frac{[ES][I]}{[ESI]} \;\;\;\mbox{・・・式4}$$
阻害剤が存在しない場合
$$ V_0 = \frac{V_{\mathrm{max}} [S]}{K_{\mathrm{m}} + [S]}$$
阻害剤が存在する場合
酵素濃度の保存則は
$$ [E]_0 = [E] + [ES] + [EI] + [ESI] \;\;\;\mbox{・・・式5}$$
式5に式3および式4を代入すると
$$[E]_0 = [E] + [ES] + \frac{[E] [I]}{K_{\mathrm{i}}} + \frac{[ES][I]}{\alpha K_{\mathrm{i}}} \;\;\;\mbox{・・・式6}$$
となります。これを変形すると
$$ [E] = \frac{[E]_0 – \left( 1 + \frac{[I]}{\alpha K_{\mathrm{i}}}\right) [ES] }{ 1 + \frac{[I]}{K_{\mathrm{i}}}} \;\;\;\mbox{・・・式7}$$
となります。
式2と式7を連立して [ES] について解くと
$$ [ES] = \frac{[E]_0 [S]}{K_{\mathrm{m}}\left(1+ \frac{[I]}{K_{\mathrm{i}} }\right) + [S] \left( 1 + \frac{[I]}{\alpha K_{\mathrm{i}} }\right)} $$
となります。
したがって阻害剤が存在する時の反応速度 \(V_I \)(\(V_I = k_{cat} [ES]\)、\(k_{cat} [E]_0 = V_{\mathrm{max}}\))は
$$ V_I = \frac{V_{\mathrm{max}} [S]}{K_{\mathrm{m}}\left(1+ \frac{[I]}{K_{\mathrm{i}} }\right) + [S] \left( 1 + \frac{[I]}{\alpha K_{\mathrm{i}} }\right)} $$
と表わされます。
\( [I] = [I]_{50}\) の時、\( V_0 = 2 V_I \) であるため、
$$ \frac{V_{\mathrm{max}} [S]}{K_{\mathrm{m}} + [S]} = \frac{2 V_{\mathrm{max}} [S]_{50}}{K_{\mathrm{m}}\left(1+ \frac{[I]_{50}}{K_{\mathrm{i}} }\right) + [S]_{50} \left( 1 + \frac{[I]_{50}}{\alpha K_{\mathrm{i}} }\right)} $$
という関係式が得られます。この式を変形すると
$$[I]_{50} = \frac{[S]_{50} + 2\frac{[S]_{50}}{[S]}K_{\mathrm m} – K_{\mathrm m}}{ \frac{K_{\mathrm m}}{K_{\mathrm i}} + \frac{[S]_{50}}{\alpha K_{\mathrm i}}}$$
となります。
基質濃度が酵素濃度に対して十分大きければ、遊離型基質濃度\([S]\)および\([S]_{50}\)を初期濃度\([S]_0\)で近似できるので、上式の\([S]\)および\([S]_{50}\)を\([S]_0\)に置換してから上式を変形すると
$$ [I]_{50} = \frac{[S]_0 + K_{\mathrm{m}} }{\frac{K_{\mathrm{m}}}{K_{\mathrm{i}}} + \frac{[S]_0}{\alpha K_{\mathrm{i}} } } $$
となります。
さらに、阻害剤濃度が酵素濃度に対して十分に過剰(\([I] \gg [EI] + [ESI]\))であれば、遊離型阻害剤濃度 \( [I]_{50}\) を全阻害剤濃度 \(\mathrm{IC}_{50} \) で近似でき、
$$ \mathrm{IC}_{50} = \frac{[S]_0 + K_{\mathrm{m}} }{\frac{K_{\mathrm{m}}}{K_{\mathrm{i}}} + \frac{[S]_0}{\alpha K_{\mathrm{i}} } } \;\;\;\mbox{・・・式1}$$
式1が導かれます。
参考文献
- 安達弥永, 安保智子, 藤島美紀, 渡邊治夫、ヒト肝ミクロソームのチトクロームP-450活性へのスギナエキスの影響と血中薬剤との相互作用予測. 生活衛生 2010, 54, 137–145. DOI: 10.11468/seikatsueisei.54.137
- Buker, S. M.; Boriack–Sjodin, P. A.; Copeland, R. A. Enzyme–Inhibitor Interactions and a Simple, Rapid Method for Determining Inhibition Modality. SLAS Discovery 2019, 24, 515–522. DOI: 10.1177/2472555219829898
- Cheng, Y.- C.; Prusoff, W. H. Relationship between the inhibition constant (KI) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem. Pharmacol. 1973, 22, 3099–3108. DOI: 10.1016/0006-2952(73)90196-2
- プロメガ株式会社「テックの一言コラム_2015年9月号 これから創薬を始める方へ ~ 酵素阻害剤編 ~」(2025年12月16日閲覧).
Kiが非常に小さい阻害剤(Tight-binding inhibitor)の場合
まとめ(引用)
強い阻害剤(\([I] \approx [E]\))のKiの具体的な算出には,線形型のHendersonプロット,あるいはMorrisonの式を用いた非線形回帰分析を行う.ただし,HendersonプロットやMorrisonの式から求まるものは見かけの \(K_{\mathrm{i}}\)(\(K^{\mathrm{app}}_{\mathrm{i}}\))であり, … \(K_{\mathrm{i}}\)への変換を要する.
Morrisonの式
遊離型阻害剤濃度 \( [I]\) を全阻害剤濃度 \([I]_{\mathrm{T}} \) で近似できない場合、Morrisonの式(Morrison equation)を使って、非線形回帰分析により見かけの \(K_{\mathrm{i}}\)値( \(K^{\mathrm{app}}_{\mathrm{i}}\))を求める(Morrison, 1969; Copeland, 2000)。
$$ \frac{V_I}{V_0} = 1 – \frac{ ([E]_0 + [I]_{\mathrm{T}}) + K^{\mathrm{app}}_{\mathrm{i}} ) – \sqrt{ ([E]_0 + [I]_{\mathrm{T}}) + K^{\mathrm{app}}_{\mathrm{i}} )^2 – 4 [E]_0 [I]_{\mathrm{T}} } }{ 2 [E]_0 } $$
拮抗阻害: $$ K^{\mathrm{app}}_{\mathrm{i}} = K_{\mathrm{i}} \left( 1 + \frac{[S]}{K_{\mathrm{m}}} \right)$$
非拮抗阻害: $$ K^{\mathrm{app}}_{\mathrm{i}} = \frac{\alpha K_{\mathrm{i}} (K_{\mathrm{m}} + [S] )}{\alpha K_{\mathrm{m}} + [S]} $$ \(\alpha = 1\) の時: $$K^{\mathrm{app}}_{\mathrm{i}} = K_{\mathrm{i}} $$
不拮抗阻害: $$ K^{\mathrm{app}}_{\mathrm{i}} = K_{\mathrm{i}} \left( 1 + \frac{K_{\mathrm{m}}} {[S]}\right)$$
参考文献
- 知名秀泰, 岡田豊、続・生物工学基礎講座 バイオよもやま話 原典からの酵素反応速度論. 生物工学会誌 2014, 92, 20–25. https://www.sbj.or.jp/sbj/sbj_vol92_no01.html
- Morrison , J. F. Kinetics of the reversible inhibition of enzyme-catalysed reactions by tight-binding inhibitors. Biochim. Biophys. Acta, Enzymol. 1969, 185, 269–286. DOI: 10.1016/0005-2744(69)90420-3
- Copeland, R. A. Tight-binding inhibitor. Enzymes: A Practical Introduction to Structure, Mechanism, and Data Analysis, 2nd ed.; Wiley, 2000, 205–317. DOI: 10.1002/0471220639.ch9
基質と阻害剤の両方がTight-bindingの場合
酵素阻害剤複合体の濃度 [EI] は以下の式で表わされる(Wang, 1995)。
$$ [EI] = \frac{ [I]_{\mathrm{T}} \{2\sqrt{(a^2 – 3b)} \cos (\Theta/3) – a \} }{ 3K_{\mathrm{i}} + \{2\sqrt{(a^2 – 3b)} \cos (\Theta/3) – a \} } $$
上式において、
$$ a = K_{\mathrm{s}} + K_{\mathrm{i}} + [S]_{\mathrm{T}} + [I]_{\mathrm{T}} – [E]_{\mathrm{T}} $$
$$ b = K_{\mathrm{i}} ([S]_{\mathrm{T}} – [E]_{\mathrm{T}}) + K_{\mathrm{s}} ([I]_{\mathrm{T}} – [E]_{\mathrm{T}}) + K_{\mathrm{s}} K_{\mathrm{i}} $$
$$ c = -K_{\mathrm{s}} K_{\mathrm{i}} [E]_{\mathrm{T}} $$
$$ \Theta = \arccos \frac{-2a^3 + 9ab – 27c}{2\sqrt{(a^2-3b)^3}} $$
参考文献
- Wang, Z.-X. An exact mathematical expression for describing competitive binding of two different ligands to a protein molecule. FEBS Lett. 1995, 360, 111–114. DOI: 10.1016/0014-5793(95)00062-E