In the world of drug discovery, where scientists are the detectives and diseases are the elusive criminals, radioligand binding assays (RLBAs) were once the Sherlock Holmes of the lab.
— Ancellin, Nicolas, “Radioligand Binding Assays: A Lost Art in Drug Discovery?”.
研究室内向けメモ。December 24, 2025改訂。
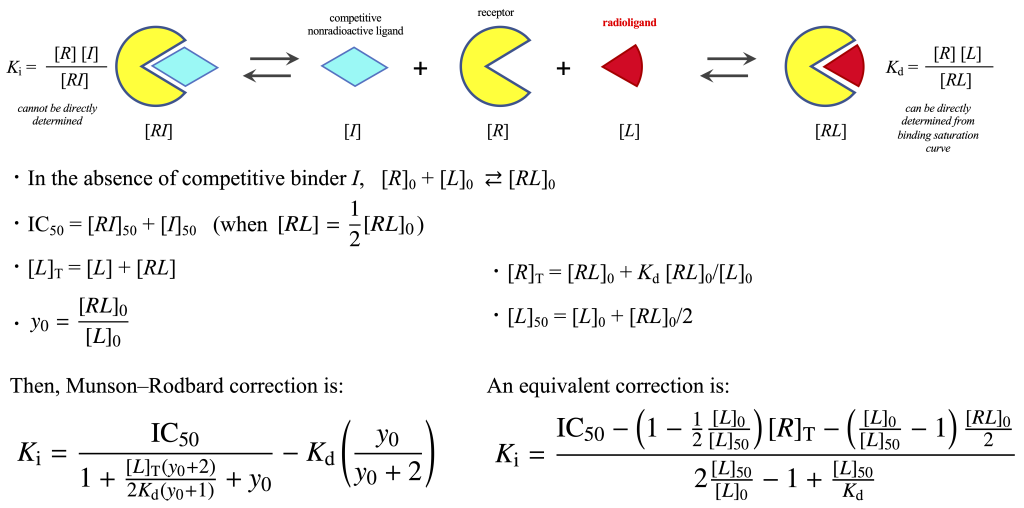
競合結合試験のIC50値から結合阻害定数\(K_{\rm i}\)を計算する方法としては、よく知られている近似的なCheng–Prusoff式の他に、厳密なMunson–Rodbard式があります。また、IC50を求める方法には非線形回帰と線形回帰があります。これらの方法で結合阻害定数\(K_{\rm i}\)を計算した時に、シミュレーションの真の\(K_{\rm i}\)値とのずれがどの程度なのかを調べました。
計算のパラメータには受容体としてプロテインキナーゼC δ-C1Bドメイン、放射性標識リガンドとして [3H]phorbol 12,13-dibutyrate([3H]PDBu)を使用した時の典型的な値を使いました: 受容体総濃度\([R]_{\textrm T} = 3.45\; \textrm{nM}\), 放射性標識リガンド総濃度\([L]_{\textrm T} = 17\; \textrm{nM}\), 放射性標識リガンドの受容体に対する解離定数\(K_{\textrm d} = 0.53\; \textrm{nM}\)。非標識リガンドの濃度範囲は、\(K_{\rm i}\) = 0.05 nMの時log [I]T が−9.021から−7.457; 0.1 nMの時−9.172から−7.459; 0.5 nMの時−8.908から−6.987; 1 nMの時−8.454から−6.496; 10 nMの時−7.495から−5.500; 100 nMの時−6.500から−4.500です(50%を挟むおおよそ−0.5刻みの5点)。
得られるIC50の値は、非線形回帰(ロジスティック関数でフィッティング)と線形回帰とでほとんど差はありませんでした。
| 真のKi値 | [I]50 (nM) | 真のIC50 (nM) | IC50 (非線形回帰、ロジスティック関数) | IC50 (線形回帰) |
| 0.05 nM | 1.51 | 3.24 | 3.18 | 3.17 |
| 0.1 nM | 3.02 | 4.75 | 4.72 | 4.68 |
| 0.5 nM | 15.1 | 16.8 | 16.8 | 16.8 |
| 1 nM | 30.2 | 31.9 | 31.9 | 31.9 |
| 10 nM | 302 | 304 | 303 | 303 |
| 100 nM | 3019 | 3020 | 3015 | 3014 |
| 真のKi値 | 真のIC50から計算したKi値 (nM) | |||
| Cheng–Prusoff | Modified Cheng–Prusoffa | Munson–Rodbard (exact) correction | IC50 – [R]T/2 correctionb | |
| 0.05 nM | 0.0980 | 0.108 | 0.0500 | 0.0502 |
| 0.1 nM | 0.143 | 0.159 | 0.100 | 0.100 |
| 0.5 nM | 0.508 | 0.561 | 0.499 | 0.499 |
| 1 nM | 0.964 | 1.07 | 1.00 | 1.00 |
| 10 nM | 9.19 | 10.2 | 10.0 | 10.0 |
| 100 nM | 91.3 | 101 | 100 | 100 |
| a [L]T の代わりに [L]50 を使用して計算した。 b \(K_{\mathrm i} = (\mathrm{IC}_{50} – [R]_\mathrm{T}/2 )/(2 [L]_{50}/[L]_{0} – 1 + [L]_{50}/K_\mathrm{d}) \). | ||||
分かったこと:
- (オリジナルの)Cheng–Prusoff式はKi値が高い時にも意外にずれが大きい。
- [L]Tの代わりに [L]50 を使った修正Cheng–Prusoff式は、Ki ≧ 10 nMの場合に真のKi値と有効数字2桁で一致するが、Ki が低い時にはずれが大きい。
- 表計算ソフトが使える現在では厳密なMunson–Rodbard補正を使わない理由はない。少なくとも [I]50 とIC50の差が開いてくるKi < 10 nMの場合は、Munson–Rodbard式を使う必要がある。
- IC50 – [R]T/2 補正では精度的にはMunson–Rodbard補正と同等。
Contents
計算に使用する数値のBinding assayからの算出方法
Binding assayの方法はSharkey & Blumberg (1985) に多少の変更点を加えています。
平衡状態での非特異的結合は無視します。
Pellet (主にγグロブリン) に対する非特異的吸着と上清との間の放射標識リガンドの分配係数 k = [pellet(nonspecific)] / ([supernatant(nonspecific)] × 437/50)
[RL]] = [pellet(total)] − k × [supernatant(total)] × 437/50
[L]T = [pellet(total)] + [supernatant(total)] × 437/50
[L]*T = [L]T/(1 + k)
[L]0 = [supernatant(total)] = ([L]T − [RL]0)/(1 + k)
[L]50 = ([L]T − [RL]0/2)/(1 + k)
[R]T = Kd [RL]0 / [L]0 + [RL]0
放射活性DPM(壊変毎分)をモル濃度 (nM) に換算する係数N:
\[
N = \frac{1}{60} \times \frac{1}{3.7 \times 10^{10}} \times \frac{1}{\mbox{比活性 (Ci/mmol)}} \times \frac{1}{10^3} \times \frac{1}{250 \times 10^{-6}} \times 10^9
\]
非特異的結合について
細胞の膜画分をbinding assayに用いる場合、膜タンパク質への低親和性結合やリン脂質への分配、分離フィルターへの吸着などの非特異的結合が起こる。通常これらの低親和性過程は不飽和であり、非特異的結合係数 (\(k\)) とfree放射リガンド濃度 \([L]\) の積としてモデル化できる (Hulme and Trevethick, 2010)。
[3H]PDBu結合試験では、ポリエチレングリコール (PEG) を添加してタンパク質を凝集させますが(PEG沈)、共沈剤としてγ-グロブリンを系に加えているため、γ-グロブリンに対する非特異的吸着が起きます(通常分配係数 k = 3–5%程度)。この非特異的吸着が [RL]0 と [L]0 にどの程度影響を与えるか計算してみたところ、k = 0の時 [RL]0 = 3.321 nM、[L]0 = 13.7 nM、k = 0.04の時 [RL]0 = 3.316 nM、[L]0 = 13.2 nMでした。リガンド濃度が十分高ければ、bound [RL] にはほとんど影響がないため、free [L] の値だけ k で補正すればよいでしょう。非標識リガンドのγ-グロブリンに対する非特異的結合については、分配係数が測れないため、考慮することができません。仮に非標識リガンドのγ-グロブリンに対する分配係数が [3H]PDBuの分配係数と等しいとすると、加えた非標識リガンドの濃度を (1 + k) で割って補正することで、[I]Tが推定できます。例えば、真のKiが10 nMのリガンドの分配係数 k = 0.04と仮定した場合、Munson–Rodbard式で計算したKi値は、補正なしで10.47 nM、補正ありで10.06 nMでした。
Cheng–Prusoff式の導出
使用するパラメータ
Total binding群
\begin{equation}
[R]_0 + [L]_0 \rightleftharpoons [RL]_0
\end{equation}
\begin{equation}
K_{\rm d} = \frac{[R]_0[L]_0}{[RL]_0}
\end{equation}
\begin{equation}
[R]_{\rm T} = [R]_0 + [RL]_0
\end{equation}
\begin{equation}
K_{\rm d} = \frac{([R]_{\rm T} – [RL]_0)[L]_0}{[RL]_0}
\end{equation}
\begin{equation}
[RL]_0 = \frac{[R]_{\rm T}[L]_0}{K_{\rm d} + [L]_0}
\end{equation}
Competitive inhibition群
\([I]\): 遊離の非標識リガンド濃度
\begin{equation}
[RI] \rightleftharpoons [I] + [R] + [L] \rightleftharpoons [RL]
\end{equation}
\begin{equation}
K_{\rm i} = \frac{[R][I]}{[RI]}
\end{equation}
\begin{equation}
[R_{\rm T}] = [RI] + [R] + [RL]
\end{equation}
\begin{equation}
[R_{\rm T}] = \frac{[R][I]}{K_{\rm i}} + [R] + [RL]
\end{equation}
\begin{equation}
[R_{\rm T}] = \left(1+\frac{[I]}{K_{\rm i}}\right)[R] + [RL]
\end{equation}
\begin{equation}
[R_{\rm T}] = \left(1+\frac{[I]}{K_{\rm i}}\right)\frac{K_{\rm d}[RL]}{[L]}+ [RL]
\end{equation}
\begin{equation}
[RL] = \frac{[R]_{\rm T}[L]}{\left(1+\frac{[I]}{K_{\rm i}}\right)K_{\rm d} + [L]}
\end{equation}
近似を使わない式の導出
50%結合阻害時
50%結合阻害時を考える。
\begin{equation}
\frac{1}{2}[RL]_0 = [RL]_{50}
\end{equation}
\begin{equation}
\frac{1}{2}\frac{[R]_{\rm T}[L]_0}{K_{\rm d} + [L]_0} = \frac{[R]_{\rm T}[L]_{50}}{\left(1+\frac{[I]_{50}}{K_{\rm i}}\right)K_{\rm d} + [L]_{50}}
\end{equation}
\begin{equation}
2\frac{K_{\rm d} }{[L]_0} + 2 = \left(1+\frac{[I]_{50}}{K_{\rm i}}\right)\frac{K_{\rm d} }{[L]_{50}}
+ 1
\end{equation}
\begin{equation}
2\frac{[L]_{50}}{[L]_0} + \frac{[L]_{50}}{K_{\rm d}} = 1+\frac{[I]_{50}}{K_{\rm i}}
\end{equation}
\begin{equation}
K_{\rm i} = \frac{[I]_{50}}{2\frac{[L]_{50}}{[L_0]} – 1 + \frac{[L]_{50}}{K_{\rm d}}} \;\;\;\;\mbox{(Goldstein and Barrett, 1987)}
= \frac{[I]_{50}}{1 + \frac{[L]_{50}}{K_{\rm d}} + 2\frac{[L]_{50}-[L]_0}{[L]_0}}
\end{equation}
Cheng–Prusoff式への変換
レセプター濃度 \([R]\) に対して \([L]\) が十分大きければ、\([L]_0 \simeq [L]_{50} \simeq [L]^{*}_{\rm T}\)なので
\begin{equation}
K_{\rm i} = \frac{[I]_{50}}{1 + \frac{[L]^{*}_{\rm T}}{K_{\rm d}}}
\end{equation}
レセプター濃度 \([R]\) に対して \([I]\) が十分大きければ、\([I]_{50}\) は50%阻害時のリガンド総濃度\(\textrm{IC}_{50}\)で近似できるので
\begin{equation}
K_{\rm i} = \frac{\textrm{IC}_{50}}{1+\frac{[L]^{*}_{\rm T}}{K_{\rm d}}} \;\;\;\mbox{(Cheng–Prusoff equation)}
\end{equation}
結合阻害曲線のシミュレーション
\([RL]_0\)の値は二次方程式を解いて求められる(\([R]_{\mathrm T} = 3.45\)、\([L]_{\mathrm T} = 17\)、\(K_{\mathrm d} = 0.53\)の時、\([RL]_0 = 3.321\))。
$$ [RL]_0 = \frac{1}{2}\left[([R]_{\rm T} + [L]_{\rm T} + K_{\rm d}) – \sqrt{([R]_{\rm T} + [L]_{\rm T} + K_{\rm d})^2 – 4[R]_{\rm T}[L]_{\rm T}}\right] $$
同様に非標識リガンド存在下での \([RL]\) は遊離型非標識リガンド濃度 \([I]\) を変数とした以下の関数で表される。
$$ [RL] = \frac{1}{2}\left\{\left[[R]_{\rm T} + [L]_{\rm T} + \left(1+\frac{[I]}{K_{\rm i}}\right)K_{\rm d}\right] – \sqrt{\left[[R]_{\rm T} + [L]_{\rm T} + \left(1+\frac{[I]}{K_{\rm i}}\right)K_{\rm d}\right]^2 – 4[R]_{\rm T}[L]_{\rm T}}\right\} $$
遊離型非標識リガンド濃度 \(\log_{10} [I]\) に対して放射リガンド結合度 \(\theta = [RL]/[RL]_0\)をプロットすると、以下のグラフを描くことができる。
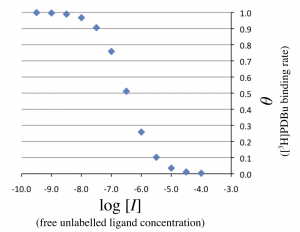
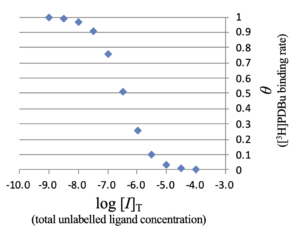
上の図1の横軸をunlabelled ligandの対数濃度 \(\log_{10} [I]_{\textrm T}\) に変更した。なお、
$$ [I]_{\mathrm T} = [I] + [RI] $$
$$ [RI] = [R]_{\mathrm{T}} – \frac{[L]_0}{[L]_{\mathrm T} – [RL]}\frac{[RL]}{[RL]_0}[R]_{\mathrm{T}} + \left( \frac{[L]_0}{[L]_{\mathrm T} – [RL]} – 1\right) [RL] \;\; .$$
data.csv
logIT,theta -9.495,0.999 -8.995,0.997 -8.495,0.990 -7.995,0.968 -7.496,0.906 -6.996,0.759 -6.498,0.512 -5.999,0.259 -5.500,0.102 -5.000,0.035 -4.500,0.011 -4.000,0.004
非線形回帰によるKiの推定
統計解析ソフトウェアRを使って非線形回帰を行う。
[I] の関数への非線形回帰
$$ \theta = \frac{1}{[RL]_0} \times \frac{1}{2}\left\{\left[[R]_{\rm T} + [L]_{\rm T} + \left(1+\frac{[I]}{K_{\rm i}}\right)K_{\rm d}\right] – \sqrt{\left[[R]_{\rm T} + [L]_{\rm T} + \left(1+\frac{[I]}{K_{\rm i}}\right)K_{\rm d}\right]^2 – 4[R]_{\rm T}[L]_{\rm T}}\right\} $$
\([I]\) の変わりに \([I]_\mathrm{T} (= [I] + [RI]) \) を使いたいが、\([RI]\) の式に \([RL]\) が含まれてしまう。ここでは、\([I] \simeq [I]_\mathrm{T} – [R]_\mathrm{T}/2) \) という簡単な補正を使用して、置換する。すると \([I]_\mathrm{T}\) の関数
$$ \theta = \frac{1}{[RL]_0} \times \frac{1}{2}\left\{\left[[R]_{\rm T} + [L]_{\rm T} + \left(1+\frac{[I]_\mathrm{T} – [R]_\mathrm{T}/2}{K_{\rm i}}\right)K_{\rm d}\right] – \sqrt{\left[[R]_{\rm T} + [L]_{\rm T} + \left(1+\frac{[I]_\mathrm{T} – [R]_\mathrm{T}/2}{K_{\rm i}}\right)K_{\rm d}\right]^2 – 4[R]_{\rm T}[L]_{\rm T}}\right\} $$
が得られる。上式において (\( [R]_{\rm T} = 3.45; [L]_{\rm T} = 17; K_{\rm d} = 0.53; [RL]_0 = 3.3213\)(単位はnM)である。
simulation <- read.csv("data.csv")
simulation$IT <- 10^(simulation$logIT + 9)
result1 <- nls(
theta ~ 1/3.3213 * 1/2 * ((3.45 + 17 + (1+ (IT - 3.45/2)/Ki)*0.53) - sqrt((3.45 + 17 + (1+ (IT - 3.45/2)/Ki)*0.53)^2 - 4*3.45*17)),
data = simulation,
start = c(Ki = 20)
)
summary(result1)
Output:
Formula: theta ~ 1/3.3213 * 1/2 * ((3.45 + 17 + (1 + (IT - 3.45/2)/Ki) *
0.53) - sqrt((3.45 + 17 + (1 + (IT - 3.45/2)/Ki) * 0.53)^2 -
4 * 3.45 * 17))
Parameters:
Estimate Std. Error t value Pr(>|t|)
Ki 10.96500 0.09913 110.6 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.003358 on 11 degrees of freedom
Number of iterations to convergence: 5
Achieved convergence tolerance: 1.366e-06
得られたKi値は10.965 nMだった(正解は11 nM)。
回帰によるIC50の推定
実験的には結合阻害曲線の裾の方は信頼性が低いので、傾きが大きな結合度50%付近のデータ点からIC50を推定して、IC50をKiに変換したい。
シグモイドへの非線形回帰
相補誤差関数(erfc)にフィッティング
$${\rm erfc}(x) = \frac{2}{\sqrt{\pi}}\int_{x}^{\infty}e^{-t^{2}}\,dt$$
(研究室に入ったころはRやExcelを使わずに、PriProbitプログラム (Sakuma, 1998) を使ってIC50を求めていました。)
Probit関数は正規分布の累積分布関数\(\Phi\)の逆関数である。相補誤差関数 erfc と\(\Phi\)には次の関係が成り立つ: \(\Phi (x) = \frac{1}{2} {\rm erfc}\left(-\frac{x}{\sqrt{2}}\right)\)。
simulation <- read.csv("data.csv")
erfc <- function(x) 2 * pnorm(x * sqrt(2), lower=FALSE)
result2 = nls(theta~1/2*erfc((logIT - logIC50)/a), data = simulation, start = c(logIC50=-6.5, a=1))
summary(result2)
Formula: $$\theta = \frac{1}{2}\cdot\mbox{erfc}\left(\frac{\log[I]_{\rm T} - \log{\rm IC}_{50}}{a}\right)$$
(※範囲を0から1にするため1/2を掛けている)
Output:
Formula: theta ~ 1/2 * erfc((logIT - logIC50)/a)
Parameters:
Estimate Std. Error t value Pr(>|t|)
logIC50 -6.476263 0.006851 -945.27 < 2e-16 ***
a 1.082295 0.013710 78.94 2.6e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.005889 on 10 degrees of freedom
Number of iterations to convergence: 5
Achieved convergence tolerance: 6.534e-07
フィッティング度合いの可視化
concpre = seq(-10,-3.5, length=100) plot(theta~logIT,data=simulation,xlim=c(-10,-3.5),ylim=c(0,1)) lines(concpre, predict(result2, newdata=list(logIT=concpre)))
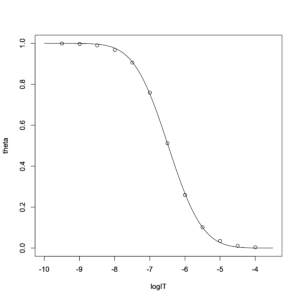
カーブの部分であまり当て嵌まりが良くない。
減少するロジスティック関数 \(1/(1 + \exp(ax))\) にフィッティング
標準シグモイド関数は$$f(x) = \frac{1}{1 + e^{-ax}}\;\;\mbox{。}$$
減少するロジスティック関数は1 − 標準シグモイド関数: $$f(x) = 1 - \frac{1}{1 + e^{-ax}} = \frac{1}{1 + e^{ax}}\;\;\mbox{。}$$
result3 = nls(theta~1/(1+exp(a*log(10)*(logIT - logIC50))), data = simulation, start = c(logIC50=-6.5, a=1)) summary(result3)
Formula: $$\theta = \frac{1}{1 + e^{a \log_{e} 10 (\log_{10}[I]_{\rm T} - \log_{10}{\rm IC}_{50})}}$$
Output:
Formula: theta ~ 1/(1 + exp(a * log(10) * (logIT - logIC50)))
Parameters:
Estimate Std. Error t value Pr(>|t|)
logIC50 -6.476238 0.001243 -5209.7 <2e-16 ***
a 0.964276 0.002346 411.1 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.001071 on 10 degrees of freedom
Number of iterations to convergence: 4
Achieved convergence tolerance: 8.128e-08
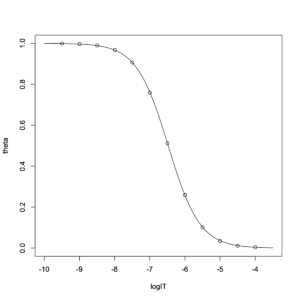
減少するロジスティック関数にシミュレーションデータは完璧に当て嵌まっているように見える。log10 IC50 = -6.476238、a = 0.964276だった。この曲線は生物学・薬理学分野で「阻害曲線」と呼ばれる。パラメータaはシグモイド曲線の傾きを記述するリガンドのヒル係数 nHである。以下に変換を示す。
まず、2つ下の節に示すようにθは
$$\theta = \frac{\frac{[L]}{[L]_0} (K_{\rm d} + [L]_0)}{\frac{K_{\rm d}}{K_{\rm i}}[I] + K_{\rm d} + [L]} $$
と表わすことができる。\([L] \simeq [L]_0\)、\([I] \simeq [I]_{\mathrm T}\)ならば
$$\theta = \frac{1}{1 + \frac{1}{K_{\rm d} + [L]_0}\frac{K_{\rm d}}{K_{\rm i}} [I]_{\mathrm T}} $$
$$\theta = \frac{1}{1 + \exp\left\{\log_{e} 10 \left[\log_{10} [I]_{\mathrm T} - \log_{10} K_{\mathrm i}\left( 1+ \frac{[L]_0}{K_\mathrm{d}} \right) \right]\right\}} $$
と書ける。Cheng–Prusoff式から\( K_{\mathrm i}\left( 1+ \frac{[L]_0}{K_\mathrm{d}} \right) \simeq \mathrm{IC}_{50} \) なので、
$$\theta = \frac{1}{1 + \exp\left[\log_{e} 10 \left(\log_{10} [I]_{\mathrm T} - \log_{10} \mathrm{IC}_{50} \right)\right]} $$
と近似的に表わされる。
実際上は相補誤差関数を使ってもほとんど同じIC50が得られているが、モデルとしてはこちらの方が優れている。
線形回帰
次に線形回帰を適用するため(Microsoft Excelが使える!)の線形グラフへの変換を示す。
非標識リガンドの対数濃度に対して \(\log_{10} \{\theta/(1- \theta)\}\) をプロットすると(ヒルプロット)、傾きが−1に近い線形グラフが得られる。
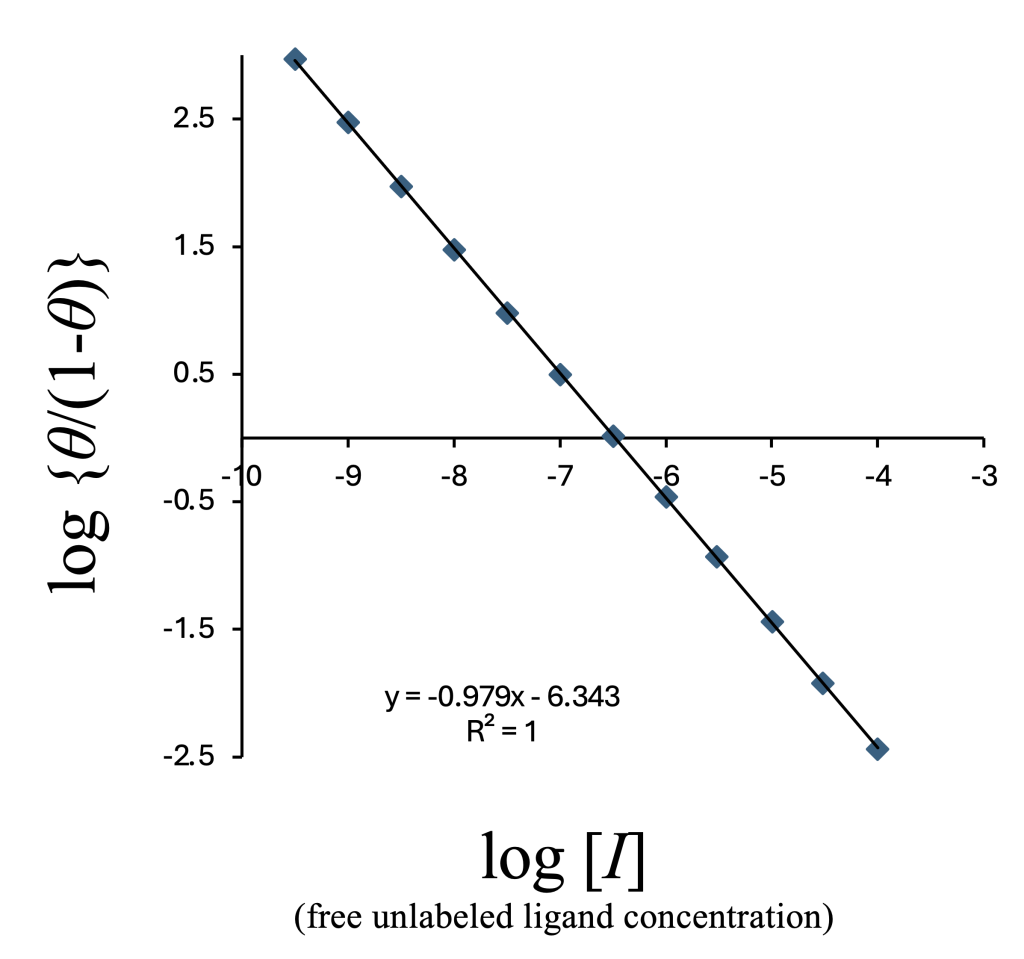
横軸を加えたリガンドの総濃度log10[I]T に変えてプロットすると以下のようになる。
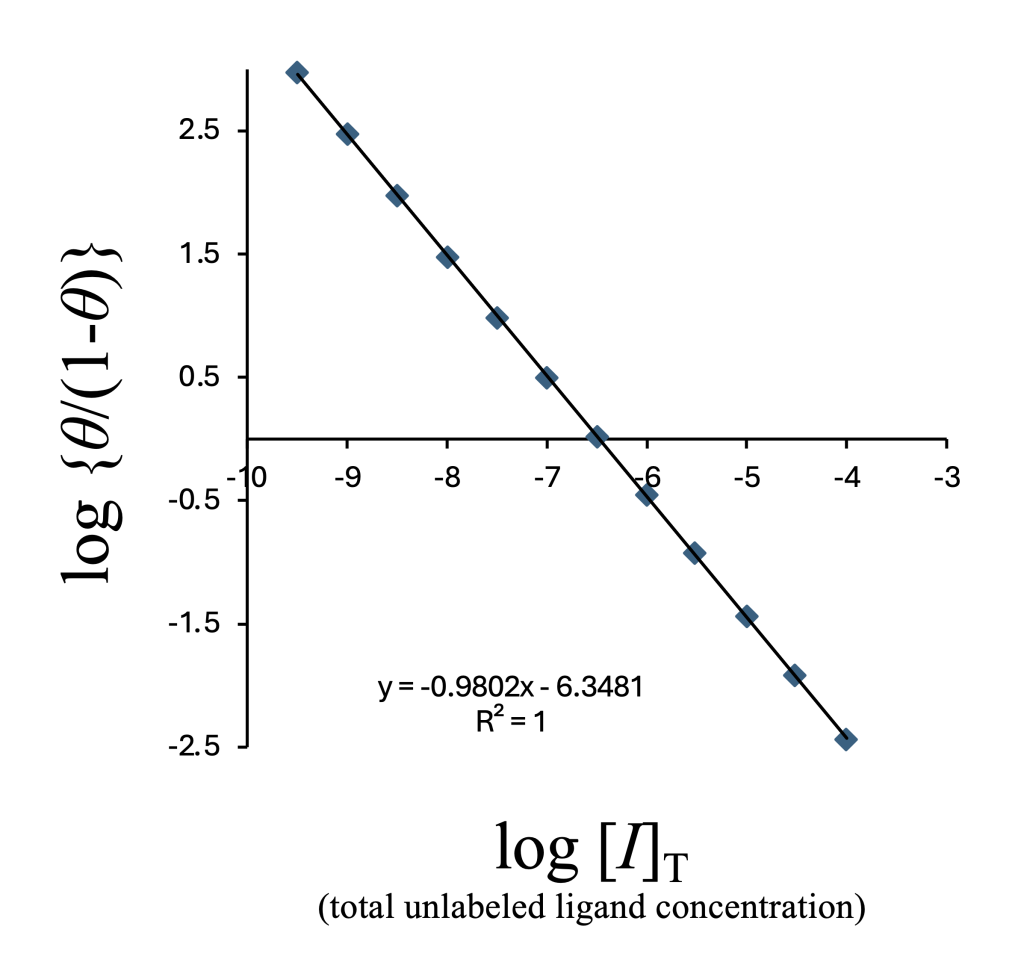
そして、Microsoft ExcelのSLOPE関数とINTERCEPT関数を使って計算したlog IC50は−6.4765となり、非線形回帰(シグモイド関数)から求めたlog IC50(-6.4762)と有効数字4桁まで一致する(nM単位に変換するとそれぞれ333.8 nMおよび334.0 nM)。
なぜ \(\log \{\theta/(1 – \theta)\}\) を \(\log [I]\) に対してプロットすると傾き \(-1\) の直線になるのか
[RL]0 と[RL] を前節のような二次方程式の解としてではなく、$$ [RL]_0 = \frac{[R]_{\rm T}[L]_0}{K_{\rm d} + [L]_0} $$
$$ [RL] = \frac{[R]_{\rm T}[L]}{\left(1+\frac{[I]}{K_{\rm i}}\right)K_{\rm d} + [L]} $$
と表すと、標識リガンド結合度 θ = [RL]/[RL]0 は、
$$\theta = \frac{[R]_{\rm T}[L]}{\left(1+\frac{[I]}{K_{\rm i}}\right)K_{\rm d} + [L]} \times \frac{K_{\rm d} + [L]_0}{[R]_{\rm T}[L]_0}$$ $$\theta = \frac{\frac{[L]}{[L]_0} (K_{\rm d} + [L]_0)}{\frac{K_{\rm d}}{K_{\rm i}}[I] + K_{\rm d} + [L]} $$
と表わされるので,
\begin{equation}
\frac{\theta}{1-\theta} = \frac{\frac{[L]}{[L]_0}(K_{\rm d} + [L]_0)}{\frac{K_{\rm d}}{K_{\rm i}}[I] + K_{\rm d} + [L] - \frac{[L]}{[L]_0}(K_{\rm d} + [L]_0)} = \frac{\frac{[L]}{[L]_0} K_{\rm d} + [L]}{\frac{K_{\rm d}}{K_{\rm i}}[I] + \left(1 - \frac{[L]}{[L]_0}\right) K_{\rm d}}
\end{equation}
という関係式が得られる。
\([L]_0 \simeq [L]\)が成り立つとすると、
\begin{equation}
\frac{\theta}{1-\theta} = \frac{K_{\rm d} + [L]}{\frac{K_{\rm d}}{K_{\rm i}}[I]}
\end{equation}
と式は簡単になる。
両辺の対数を取る(ここでは常用対数)と、freeのリガンド対数濃度 \(\log10[I]\) に対して傾き\(-1\)の直線関係になる。
\begin{equation}
\log_{10} \left(\frac{\theta}{1-\theta}\right) = -\log_{10} [I] -\log_{10} K_{\rm d} + \log_{10} K_{\rm i} + \log_{10} (K_{\rm d} + [L]) \simeq -\log_{10} [I] + \log_{10} \mathrm{IC}_{50}
\end{equation}
上式において [L] は変数 [I] に依存する。
ロジット関数(\(\log \{p/(1-p)\}\))とシグモイド関数は逆関数の関係にある。
結合度θからKi値への簡易な変換
結合阻害が50%を切らない程弱いリガンドについて、1点から\(K_{\rm i}\)を計算する方法として
\begin{equation}
\frac{\theta}{1-\theta} = \frac{K_{\rm d} + [L]}{\frac{K_{\rm d}}{K_{\rm i}}[I]}
\end{equation}
を変形すると、
\begin{equation}
K_{\rm i} = \left(\frac{\theta}{1-\theta}\right) \frac{K_{\rm d}[I]}{K_{\rm d} + [L]}
\end{equation}
レセプター濃度 \([R]\) に対して \([I]\) が十分大きければ(弱いリガンドなのでこれを満たす)、 \([I]\) はリガンド総濃度 \([I]_{\textrm T}\) で近似できるので
\begin{equation}
K_{\rm i} = \left(\frac{\theta}{1-\theta}\right) \frac{K_{\rm d}[I]_{\rm T}}{K_{\rm d} + [L]}
\end{equation}
厳密な変換には後述のDandlikerの式を使用する。
非標識リガンドの結合能が高い(Tight-binding ligand)の場合
IC50に対する補正
レセプター濃度 \([R]\) に対して \([I]\) が十分大きくない場合 (非標識リガンドの結合能が標識リガンド [3H]PDBuの結合と同等あるいはそれ以上の場合)、\([I]\) をリガンド総濃度 \([I]_{\rm T}\) で近似できない。したがって、
$$ [I]_{50} = \mathrm{IC}_{50} - [RI]_{50} $$
の \([RI]_{50} \)を計算したい。
実験的には放射活性から \([RL]_0\)、\([L]_{0}\)を測定でき、それらの値と既知のKd値から \([L]_{50} = [L]_{0} + [RL]_{0}/2\)、\([R]_{\mathrm{T}} = [RL]_0 (1 + K_{\mathrm d}/[L]_0)\)、\([RL]_{50} = [RL]_{0}/2\)を計算できる。
まず、以下の2つの保存式を考える。
Iが存在しない時: $$ [R]_{\mathrm{T}} = [R]_{0} + [RL]_{0} $$
Iの濃度が \([I]_{50}\)の時: $$ [R]_{\mathrm{T}} = [R]_{50} + [RL]_{50} + [RI]_{50} $$
標識リガンドLの平衡を考えると
$$K_{\mathrm d} = \frac{[R]_0[L]_0}{[RL]_0} = \frac{[R]_{50}[L]_{50}}{[RL]_{50}} $$
が成り立っている。この式に \( [R]_{0} = [R]_{\mathrm{T}} - [RL]_{0}\)および\( [R]_{50} = [R]_{\mathrm{T}} - [RL]_{50} - [RI]_{50}\)を代入して変形すると、
$$ [RI]_{50} = [R]_{\mathrm{T}} - \frac{[L]_0}{[L]_{50}}\frac{[RL]_{50}}{[RL]_0}[R]_{\mathrm{T}} + \left( \frac{[L]_0}{[L]_{50}} - 1\right) [RL]_{50} $$
となる。\(\frac{[RL]_{50}}{[RL]_0} = 1/2\) なので、
$$ [RI]_{50} = \left( 1 - \frac{1}{2} \frac{[L]_0}{[L]_{50}} \right)[R]_{\mathrm{T}} + \left( \frac{[L]_0}{[L]_{50}} - 1\right) [RL]_{50} $$
となる。したがって、補正式
$$ K_{\rm i} = \frac{\mathrm{IC}_{50} - \left( 1 - \frac{1}{2} \frac{[L]_0}{[L]_{50}} \right)[R]_{\mathrm{T}} - \left( \frac{[L]_0}{[L]_{50}} - 1\right) \frac{[RL]_{0}}{2} }{2\frac{[L]_{50}}{[L]_0} - 1 + \frac{[L]_{50}}{K_{\rm d}}} $$
が導かれる。この補正式から得られるKi値は厳密な値であり、次節のMunson–Rodbard補正と等価である。
もし、標識リガンド濃度がレセプター濃度に対して十分過剰で\( [L]_0 \approx [L]_{50}\) という近似を使えるとすると、上式の右辺の分子はより単純になり、
$$ K_{\rm i} = \frac{\mathrm{IC}_{50} - \frac{[R]_{\mathrm{T}}}{2}} {2\frac{[L]_{50}}{[L]_0} - 1 + \frac{[L]_{50}}{K_{\rm d}}} $$
と書くことができる。実際上は標識リガンド濃度が十分過剰でない場合でも、この簡単な補正で得られるKiで精度的に全く問題ない。
Munson–Rodbard補正
Munson–Rodbard式からIC50(総濃度)を使用して(\([I]_{50} \simeq \textrm{IC}_{50}\) の近似を使わずに)\(K_{\textrm i}\) を厳密に算出できる (Munson ad Rodbard, 1988; Huang, 2003)。
\(y_0 = [RL]_0/[L]_0\) とすると、
\begin{equation}
K_{\rm i} = \frac{\textrm{IC}_{50}}{1+ \frac{[L]_{\rm T} (y_0 + 2)}{2 K_{\rm d} (y_0 + 1)} + y_0} - K_{\rm d} \left(\frac{y_0}{y_0 + 2}\right) \;\;\;\;\mbox{(Eq.26; Munson–Rodbard式) }
\end{equation}
\(y_0\)が非常に小さければ、式26はCheng–Prusoff式へと帰着する。
Munson–Rodbard式の導出
\(K_1 = 1/K_{\rm d}\), \(K_2 = 1/K_{\rm i}\) と定義する。
\begin{equation}
[RL] = K_1 [R] [L]\;\;\;\;\mbox{(Eq.27)}
\end{equation}
\begin{equation}
[RI] = K_2 [R] [I]\;\;\;\;\mbox{(Eq.28)}
\end{equation}
保存則から
\begin{equation}
[L]_{\rm T} = [RL] + [L]\;\;\;\;\mbox{(Eq.29)}
\end{equation}
\begin{equation}
[I]_{\rm T} = [RI] + [I]\;\;\;\;\mbox{(Eq.30)}
\end{equation}
\begin{equation}
[R]_{\rm T} = [RI] + [R] + [RL] = K_2 [R] [I] + [R] + K_1 [R] [L] = [R] (1+ K_1[L] + K_2 [I])\;\;\;\;\mbox{(Eq.31)}
\end{equation}
阻害剤が存在しない場合と50%阻害時の条件を考える。
阻害剤が存在しない場合の比を \([RL]_0/[L]_0 = y_0\) と定義すると式29から、
\begin{equation}
[L]_{\rm T} = [L]_0 (1 + y_0)\;\;\;\;\mbox{(Eq.32)}
\end{equation}
\begin{equation}
[L]_0 =\frac{[L]_{\rm T}}{1 + y_0}\;\;\;\;\mbox{(Eq.33)}
\end{equation}
したがって、
\begin{equation}
[RL]_0 = \frac{ y_0 [L]_{\rm T}}{1 + y_0}\;\;\;\;\mbox{(Eq.34)}
\end{equation}
50%阻害時は、
\begin{equation}
[RL]_{50} = \frac{ y_0 [L]_{\rm T}}{2 (1 + y_0)}\;\;\;\;\mbox{(Eq.35)}
\end{equation}
Eq.29から、
\begin{equation}
[L]_{50} = [L]_{\rm T} - [RL]_{50} = \frac{ [L]_{\rm T} (2 + y_0) }{2 (1 + y_0)}\;\;\;\;\mbox{(Eq.36)}
\end{equation}
Eq.27から50%阻害時のfreeのレセプターを求めると、
\begin{equation}
[R]_{50} = \frac{[RL]_{50}}{K_1 [L]_{50}} = \frac{y_0}{K_1 (y_0 + 2)}\;\;\;\;\mbox{(Eq.37)}
\end{equation}
Eq.28, 30から、
\begin{equation}
\textrm{IC}_{50} = [I]_{{\rm T} 50} = [RI]_{50} + [I]_{50} = [I]_{50}(1+K_2 [R]_{50})\;\;\;\;\mbox{(Eq.38)}
\end{equation}
Eq.37をEq.38に代入すると、
\begin{equation}
[I]_{50} = \frac{\textrm{IC}_{50}}{1+\left(\frac{K_2}{K_1}\right)\left(\frac{y_0}{y_0+2}\right)}\;\;\;\;\mbox{(Eq.39)}
\end{equation}
Eq.31を \([R]\) について解いてEq.27に代入すると、
\begin{equation}
[RL] = \frac{K_1 [R]_{\rm T} [L] }{1+ K_1 [L] + K_2 [I]}\;\;\;\;\mbox{(Eq.40)}
\end{equation}
阻害剤が存在しない時、Eq.40はEq.34, 33から、
\begin{equation}
[R]_{\rm T} = y_0 \left(\frac{1}{K_1} + \frac{[L]_{\rm T}}{1 + y_0}\right)\;\;\;\;\mbox{(Eq.41)}
\end{equation}
50%阻害時、Eq.40は、
\begin{equation}
[RL]_{50} = \frac{K_1 [R]_{\rm T} [L]_{50} }{1+ K_1 [L]_{50} + K_2 [I]_{50}}\;\;\;\;\mbox{(Eq.42)}
\end{equation}
Eq.42を\(1/K_2\)について解く。
\begin{equation} \frac{1}{K_2} = \frac{[I]_{50}}{\frac{K_1[R]_{T}[L]_{50}}{[RL]_{50}} - K_1[L]_{50} - 1} \end{equation}
Eq.39から \([I]_{50}\)を代入して整理する。
\begin{equation} \frac{1}{K_2} + \frac{1}{K_1}\left(\frac{y_0}{y_0+2}\right) = \frac{\mathrm{IC}_{50}}{\frac{K_1[R]_{T}[L]_{50}}{[RL]_{50}} - K_1[L]_{50} - 1} \end{equation}
上の式の右辺の分母に、Eq.36から\([L]_{50}\)、Eq.41から \([R]_{\rm T}\)、そして \(\frac{[L]_{50}}{[RL]_{50}} = \frac{y_0+2}{y_0} \) を代入すると、
\begin{equation} \mbox{右辺の分母} = K_1 \times y_0\left(\frac{1}{K_1} + \frac{[L]_\mathrm{T}}{y_0+1}\right) \times \frac{y_0+2}{y_0} - K_1\frac{[L]_\mathrm{T}(y_0+2)}{2(y_0+1)} - 1 \end{equation}
\begin{equation} = 2+ y_0 + K_1\frac{[L]_\mathrm{T}(y_0+2)}{y_0+1} - K_1\frac{[L]_\mathrm{T}(y_0+2)}{2(y_0+1)} - 1 \end{equation}
\begin{equation} = 1+ K_1\frac{[L]_\mathrm{T}(y_0+2)}{2(y_0+1)} + y_0 \end{equation}
したがって、
\begin{equation}
\frac{1}{K_2} = \frac{\textrm{IC}_{50}}{1+ \frac{[L]_{\rm T} (y_0 + 2)}{2 \left(\frac{1}{K_1}\right) (y_0 + 1)} + y_0} - \left(\frac{1}{K_1}\right) \left(\frac{y_0}{y_0 + 2}\right)\;\;\;\;\mbox{(Eq.43)}
\end{equation}
最後に\(1/K_2 = K_{\rm i}\), \(1/K_1 = K_{\rm d}\)を戻すとEq.26となる。
近似を使わずに1点からKi値を計算する方法
Dandlikerの式
阻害実験のそれぞれのデータ点から\(K_{\rm i}\)を算出できる (Dandliker, 1981)。
\(\chi = [RL]/[L]\) とする (\([L]\)の値は \([L] = [L]_{\rm T} - [RL]\) と計算) と、
\begin{equation}
K_i = \frac{[I]_{\rm T} K_d \chi}{[R]_{\rm T} - \frac{[L]_{\rm T}\chi}{1 + \chi} - K_d \chi} - K_d \chi\;\;\;\;\mbox{(Eq.44)}
\end{equation}
また、\(f_b = [RL]/[L]_{\rm T}\) とすると、\(\chi = f_b/(1-f_b)\) なので、
\begin{equation}
K_{\rm i} = \frac{[I]_{\rm T} K_{\rm d} f_b}{[R]_{\rm T}(1 - f_b) - K_{\rm d} f_b - [L]_{\rm T} f_b (1 - f_b)} - \frac{K_{\rm d} f_b}{ 1 - f_b}\;\;\;\;\mbox{(Eq.45)}
\end{equation}
Eq.45はHuang, 2003の式 (11) を変形したものです。
Dandlikerの式の導出
先程と同様に、\(K_1 = 1/K_{\rm d}\), \(K_2 = 1/K_{\rm i}\)と定義する。
\begin{equation}
\chi = \frac{[RL]}{[L]} = K_1 ([R]_{\rm T} - [RL] - [RI])\;\;\;\;\mbox{(Eq.46)}
\end{equation}
\begin{equation}
\frac{[RI]}{[I]} = K_2 ([R]_{\rm T} - [RL] - [RI])\;\;\;\;\mbox{(Eq.47)}
\end{equation}
\begin{equation}
[L]_{\rm T} = [RL] + [L]\;\;\;\;\mbox{(Eq.48)}
\end{equation}
\begin{equation}
[I]_{\rm T} = [RI] + [I]\;\;\;\;\mbox{(Eq.49)}
\end{equation}
\begin{equation}
[RL] =\frac{[L]_{\rm T}\chi}{1 + \chi}\;\;\;\;\mbox{(Eq.50)}
\end{equation}
\begin{equation}
[L] =\frac{[L]_{\rm T}}{1 + \chi}\;\;\;\;\mbox{(Eq.51)}
\end{equation}
Eq.46から、
\begin{equation}
[RI] = [R]_{\rm T} - [RL] - \frac{\chi}{K_1} = [R]_{\rm T} - \frac{[L]_{\rm T}\chi}{1 + \chi} - \frac{\chi}{K_1}\;\;\;\;\mbox{(Eq.52)}
\end{equation}
Eq.47を \([I]\) について解くと
\begin{equation}
[I] = \frac{[RI]}{K_2} \times \frac{1}{[R]_{\rm T} - [RL] - [RI]}\;\;\;\;\mbox{(Eq.53)}
\end{equation}
\([RI] = [R]_{\rm T} - [RL] - \frac{\chi}{K_1}\)なので、
\begin{equation}
[I] = \frac{[R]_{\rm T} - [RL] - \frac{\chi}{K_1}}{K_2} \times \frac{1}{\frac{\chi}{K_1}} = \frac{K_1}{K_2\chi}\left([R]_{\rm T} - \frac{[L]_{\rm T}\chi}{1 + \chi} - \frac{\chi}{K_1}\right)\;\;\;\;\mbox{(Eq.54)}
\end{equation}
Eq.52とEq.54をEq.49に代入すると、
\begin{equation}
[I]_{\rm T} = \left(1 + \frac{K_1}{K_2\chi}\right) \left([R]_{\rm T} - \frac{[L]_{\rm T}\chi}{1 + \chi} - \frac{\chi}{K_1}\right)\;\;\;\;\mbox{(Eq.55)}
\end{equation}
Eq.55を\(1/K_2\)について解くと、
\begin{equation}
K_i = \frac{1}{K_2} = \frac{[I]_{\rm T} K_d \chi}{[R]_{\rm T} - \frac{[L]_{\rm T}\chi}{1 + \chi} - K_d \chi} - K_d \chi\;\;\;\;\mbox{(Eq.56)}
\end{equation}
References
- Sharkey, N. A.; Blumberg, P. M. Highly lipophilic phorbol esters as inhibitors of specific [3H]phorbol 12,13-dibutyrate binding. Cancer Res. 1985, 45, 19–24. [URL] [PMID]: 3855281.
- Dandliker, W. B.; Hsu, M.-L.; Levin, J.; Rao, R. Equilibrium and kinetic inhibition assays based upon fluorescence polarization. Methods Enzymol. 1981, 74, 3–28. DOI: 10.1016/0076-6879(81)74003-5. PMID: 7321886.
- Goldstein, A.; Barrett, R. W. Ligand dissociation constants from competition binding assays: errors associated with ligand depletion. Mol. Pharmacol. 1987, 31, 603–609. [URL] PMID: 3600604.
- Hulme, X. C.; Trevethick, M. A. Ligand binding assays at equilibrium: validation and interpretation. Br. J. Pharmacol. 2010, 161, 1219–1237. DOI: 10.1111/j.1476-5381.2009.00604. PMID: 20132208.
- Huang, X. Equilibrium competition binding assay: inhibition mechanism from a single dose response. J. Ther. Biol. 2003, 225, 369–376. DOI: 10.1016/S0022-5193(03)00265-0. PMID: 14604589.
- Munson, P. J.; Rodbard, D. An exact correction to the Cheng-Prusoff correction. J. Receptor Res. 1988, 8, 533–546. DOI: 10.3109/10799898809049010. PMID: 3385692.
おまけ: 実際の実験データの処理
Low-affinity ligand
3H標識リガンド(比活性18.7 Ci/mmol)と非標識リガンドとの競合結合試験で得られた以下のデータを処理します。放射活性の単位はdpm(壊変毎分; Bqは壊変毎秒)です。
| GROUP | log10 [I]T | pellet (dpm) | supernatant (dpm) (50 μL) |
| Total binding | — | 36758 | 16101 |
| Total binding | — | 37325 | 17380 |
| Total binding | — | 36584 | 16934 |
| Total binding | — | 38455 | 15247 |
| Total binding | — | 33998 | 16772 |
| Nonspecific binding | — | 5592 | 20072 |
| Nonspecific binding | — | 4794 | 18772 |
| Unlabeled ligand (I) | -6.5 | 35734 | — |
| Unlabeled ligand (I) | -6.5 | 35884 | — |
| Unlabeled ligand (I) | -6.5 | 32866 | — |
| Unlabeled ligand (I) | -6 | 33393 | — |
| Unlabeled ligand (I) | -6 | 33204 | — |
| Unlabeled ligand (I) | -6 | 34506 | — |
| Unlabeled ligand (I) | -5.5 | 28644 | — |
| Unlabeled ligand (I) | -5.5 | 31701 | — |
| Unlabeled ligand (I) | -5.5 | 30276 | — |
| Unlabeled ligand (I) | -5 | 22413 | — |
| Unlabeled ligand (I) | -5 | 22516 | — |
| Unlabeled ligand (I) | -5 | 21133 | — |
| Unlabeled ligand (I) | -4.5 | 12318 | — |
| Unlabeled ligand (I) | -4.5 | 12711 | — |
| Unlabeled ligand (I) | -4.5 | 11368 | — |
- supernatantの値に437/50を掛けて、上清全体の放射活性に変換する。
- 全放射活性 = Total binding群のpellet + supernatant (全体)、を計算する。
- Nonspecific binding群のpelletをsupernatant(全体)で割って、非特異的吸着の分配係数 k を計算する: k = 0.0296。
- Total binding群のspecific binding = pellet − k × supernatant(全体)、を計算する。
- Unlabeled ligand群のspecific binding = pellet − k × (全放射活性 − pellet) を計算する。
- 放射活性 (dpm) をテストチューブ内のモル濃度 (nM) に変換する。係数 \(N = \frac{1}{60} \times \frac{1}{3.7 \times 10^{10}} \times \frac{1}{\mbox{比活性 (Ci/mmol)}} \times \frac{1}{10^3} \times \frac{1}{250 \times 10^{-6}} \times 10^9\)
- Unlabeled ligand群のそれぞれのデータについて θ = pellet (nM) / 〈Total binding群のspecific binding([RL]0)の平均値〉を計算する。
- \(\log_{10} \{\theta/(1 - \theta)\}\) を計算する。
処理したデータ
| GROUP | log10 [I]T | bound (nM) | free (nM) | θ | log10 {θ/(1 − θ)} |
| Total binding(平均) | — | 3.105 ([RL]0) | 13.88 ([L]0) | — | — |
| Unlabeled ligand (I) | -6.5 | 3.017 | — | 0.9715 | 1.533 |
| Unlabeled ligand (I) | -6.5 | 3.032 | — | 0.9763 | 1.615 |
| Unlabeled ligand (I) | -6.5 | 2.732 | — | 0.8798 | 0.865 |
| Unlabeled ligand (I) | -6 | 2.785 | — | 0.8967 | 0.939 |
| Unlabeled ligand (I) | -6 | 2.766 | — | 0.8907 | 0.911 |
| Unlabeled ligand (I) | -6 | 2.895 | — | 0.9323 | 1.139 |
| Unlabeled ligand (I) | -5.5 | 2.313 | — | 0.7448 | 0.465 |
| Unlabeled ligand (I) | -5.5 | 2.616 | — | 0.8426 | 0.729 |
| Unlabeled ligand (I) | -5.5 | 2.475 | — | 0.7970 | 0.594 |
| Unlabeled ligand (I) | -4.5 | 1.694 | — | 0.5456 | 0.079 |
| Unlabeled ligand (I) | -4.5 | 1.704 | — | 0.5489 | 0.085 |
| Unlabeled ligand (I) | -4.5 | 1.567 | — | 0.5047 | 0.008 |
| Unlabeled ligand (I) | -4 | 0.692 | — | 0.2228 | -0.543 |
| Unlabeled ligand (I) | -4 | 0.731 | — | 0.2354 | -0.512 |
| Unlabeled ligand (I) | -4 | 0.698 | — | 0.1924 | -0.623 |
ロジスティック関数にフィッティングしてIC50を推定〔推奨〕
logIT <- c(-6.5,-6.5,-6.5,-6,-6,-6,-5.5,-5.5,-5.5,-5,-5,-5,-4.5,-4.5,-4.5) theta <- c(0.9715, 0.9763, 0.8798, 0.8967, 0.8907, 0.9323, 0.7448, 0.8426, 0.7970, 0.5456, 0.5489, 0.5047, 0.2228, 0.2354, 0.1924) result <- nls(theta~1/(1+exp(a*log(10)*(logIT - logIC50))),start = c(logIC50=-5, a=1)) summary(result)
Output:
Formula: theta ~ 1/(1 + exp(a * log(10) * (logIT - logIC50)))
Parameters:
Estimate Std. Error t value Pr(>|t|)
logIC50 -4.97382 0.02644 -188.15 < 2e-16 ***
a 1.07378 0.06989 15.37 1.03e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.04024 on 13 degrees of freedom
Number of iterations to convergence: 6
Achieved convergence tolerance: 1.317e-06
confint(result, level=0.95)
Output:
2.5% 97.5%
logIC50 -5.0301661 -4.916613
a 0.9269206 1.247572
可視化:
concpre = seq(-8.5,-3.5, length=100) plot(theta~logIT,xlim=c(-10,-3.5),ylim=c(0,1)) lines(concpre, predict(result, newdata=list(logIT=concpre)))
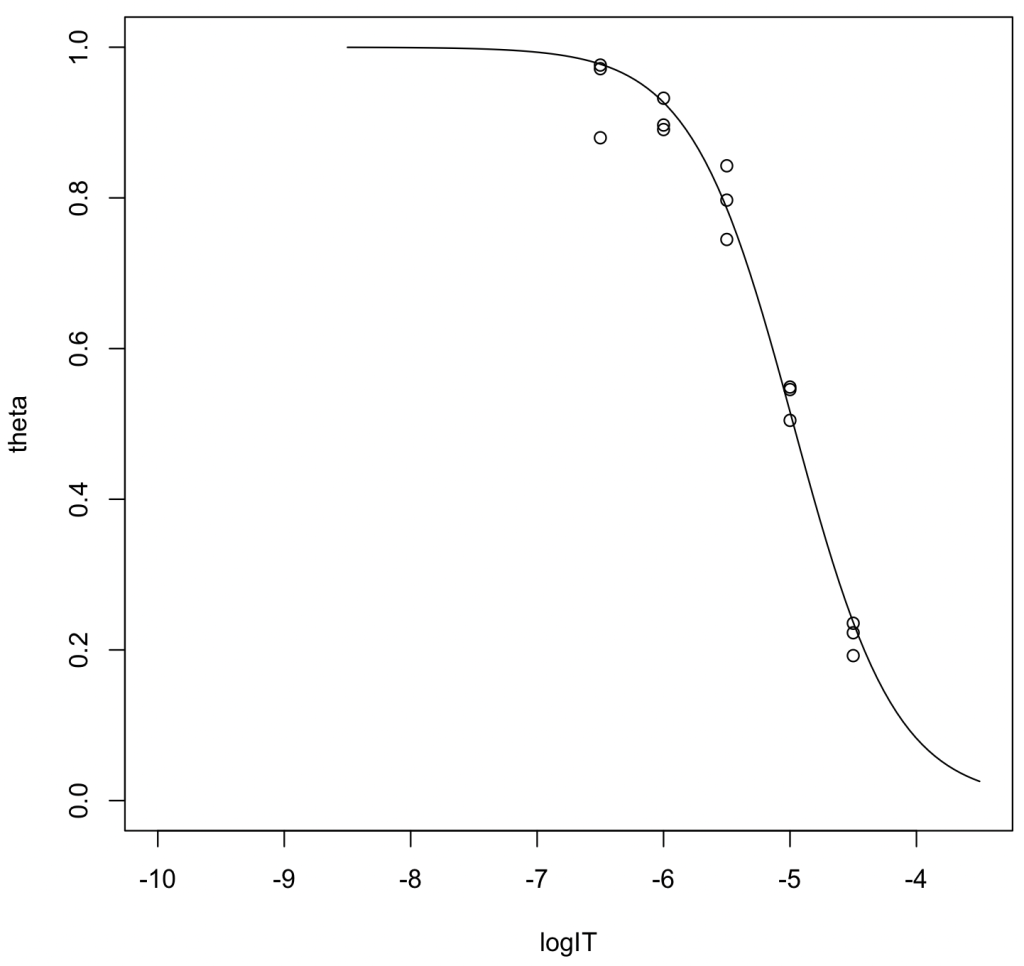
推定IC50値は10,621 nM(95%CI: 9,329–12,117)、ヒル係数は1.07だった。
Kiへの変換
非標識リガンドについても [3H]PDBuと同じ分配係数で非特異的結合が起こると仮定する。すると、
$$ \mathrm{IC}_{50} = (1 + k) [I]_{50} + [RI]_{50} $$
$$ [I]_{50} = \frac{1}{1+ k} (\mathrm{IC}_{50} - [RI]_{50}) $$
なので、\(\mathrm{IC}_{50}\)を\(K_\mathrm{i}\) に変換する以下の厳密な補正式が得られる。
$$ K_{\rm i} = \frac{\frac{1}{1 + k} \left[\mathrm{IC}_{50} - \left( 1 - \frac{1}{2} \frac{[L]_0}{[L]_{50}} \right)[R]_{\mathrm{T}} - \left( \frac{[L]_0}{[L]_{50}} - 1\right) \frac{[RL]_{0}}{2} \right] }{2\frac{[L]_{50}}{[L]_0} - 1 + \frac{[L]_{50}}{K_{\rm d}}} $$
この場合、非標識リガンドの親和性が弱く、\(\mathrm{IC}_{50} \gg [RI]_{50}\)が成り立つので、 以下の近似が成り立つ。
$$ [I]_{50} \simeq \frac{1}{1+ k} \mathrm{IC}_{50} $$
$$ K_{\rm i} = \frac{\frac{1}{1 + k} \mathrm{IC}_{50} }{2\frac{[L]_{50}}{[L]_0} - 1 + \frac{[L]_{50}}{K_{\rm d}}} $$
厳密な式で得られた\(K_\mathrm{i}\) は 340.6 nM(95% CI: 299.1–388.6)だった。近似式で得られた\(K_\mathrm{i}\) は 340.7 nMであり、違いがないことが分かった。
log10 {θ/(1 − θ)} 変換から線形回帰でIC50を推定〔次に推奨 ※Microsoft Excelしか使えない時〕
5つの濃度全てを使用
logIT <- c(-6.5,-6.5,-6.5,-6,-6,-6,-5.5,-5.5,-5.5,-5,-5,-5,-4.5,-4.5,-4.5) logit <- c(1.533, 1.615, 0.865, 0.939, 0.911, 1.139, 0.465, 0.729, 0.594, 0.079, 0.085, 0.008, -0.543, -0.512, -0.623) result_lm <- lm(logit ~ logIT) summary(result_lm)
Output:
Call:
lm(formula = logit ~ logIT)
Residuals:
Min 1Q Median 3Q Max
-0.56720 -0.04945 -0.00430 0.10460 0.24340
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.72070 0.40386 -11.69 2.86e-08 ***
logIT -0.94660 0.07283 -13.00 7.98e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1995 on 13 degrees of freedom
Multiple R-squared: 0.9285, Adjusted R-squared: 0.923
F-statistic: 168.9 on 1 and 13 DF, p-value: 7.975e-09
高濃度側の3つの濃度を使用
logIT_a <- c(-5.5,-5.5,-5.5,-5,-5,-5,-4.5,-4.5,-4.5) logit_a <- c(0.465, 0.729, 0.594, 0.079, 0.085, 0.008, -0.543, -0.512, -0.623) result_lm_a <- lm(logit_a ~ logIT_a) summary(result_lm_a)
Output:
Call:
lm(formula = logit_a ~ logIT_a)
Residuals:
Min 1Q Median 3Q Max
-0.144000 -0.023333 0.003333 0.047667 0.120000
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.7453 0.3396 -16.92 6.18e-07 ***
logIT_a -1.1553 0.0677 -17.07 5.82e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.08292 on 7 degrees of freedom
Multiple R-squared: 0.9765, Adjusted R-squared: 0.9732
F-statistic: 291.2 on 1 and 7 DF, p-value: 5.819e-07
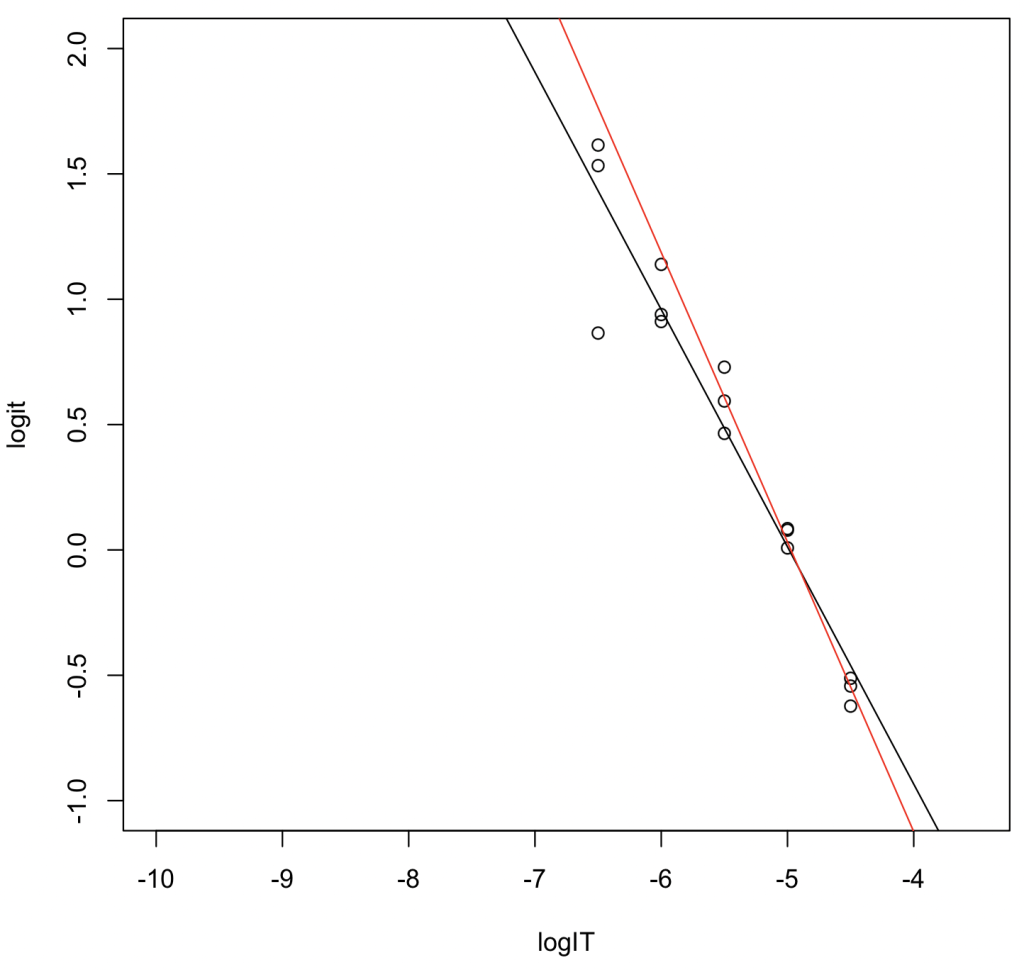
黒線(濃度5点): \( y = -0.94660 x - 4.72070\). \(R^2 = 0.929\). log10 IC50 = -4.72070/0.94660 = -4.987006。nMに変換するとIC50 = 10,304 nM。
赤線(濃度3点): \( y = -1.1553 x - 5.7453\). \(R^2 = 0.977\). log10 IC50 = -5.7453/1.1553 = -4.972994。nMに変換するとIC50 = 10,642 nM。
データ数が少ない濃度3点から推定したIC50値の方が、非線形回帰から推定したIC50値に近い結果が得られた。線形変換するとシグモイドの裾の方のデータ点を過大評価してしまうことが分かる。
前節と同じ近似式で変換したKi は濃度5点からが330.5 nM、濃度5点からが341.3 nMだった。
GraphPad Prismの方法
参考: Equation: One site - Ligand depletion — GraphPad Prism 10
有償の統計解析ソフトウェアGraphPad Prism 10に実装されている方法に則って解析を行ってみました(放射活性の単位はCPMではなくDPMを使用)。"One site - Ligand depletion" モデルは、遊離型放射リガンド濃度 ≒ 全放射リガンド濃度、の近似が使えない場合に適用されます。
基本的には「結合阻害曲線のシミュレーション」節で示した式
$$ [RL] = \frac{1}{2}\left\{\left[[R]_{\rm T} + [L]_{\rm T} + \left(1+\frac{[I]}{K_{\rm i}}\right)K_{\rm d}\right] - \sqrt{\left[[R]_{\rm T} + [L]_{\rm T} + \left(1+\frac{[I]}{K_{\rm i}}\right)K_{\rm d}\right]^2 - 4[R]_{\rm T}[L]_{\rm T}}\right\} $$
に対して、非特異的結合を考慮して放射活性はCPM単位のまま非線形回帰を行っています。Total binding群とnon-specific binding群の放射活性の値は使用しません。ここではCPMではなくDPM単位を使用しているので比活性SpActの単位は dpm/fmol です。
パラメータ
- Hot = [L]T = 17.41 [nM] = 180718 [DPM]
- KdNM = Kd = 0.53 [nM]
- SpAct = 18.7 [Ci/mmol] = 41.514 [dpm/fmol]
- Vol = 0.25 [mL]
モデル
\(KdDPM=KdNM * SpAct * Vol * 1000 \)
\(R = 1 + NS\) ;
\(S=[1+10^{(X-LogKi)}] * KdDPM+Hot\)
\(a=-1 * R\)
\(b=R * S+NS * Hot + Bmax\)
\(c= -1*Hot*(S*NS + Bmax) \)
\(Y= \frac{-b + \sqrt{b^2-4*a*c}}{2*a} \)
X <- c(-6.5,-6.5,-6.5,-6,-6,-6,-5.5,-5.5,-5.5,-5,-5,-5,-4.5,-4.5,-4.5)
Y <- c(35734, 35884, 32866, 33393, 33204, 34506, 28643, 31701, 30276, 22413, 22516, 21133, 12318, 12711, 11368)
Hot <- 180718
KdNM <- 0.53
SpAct <- 41.514
Vol <- 0.25
binding_model <- function(X, LogKi, Bmax, NS, Hot, KdNM, SpAct, Vol) {
KdDPM <- KdNM * SpAct * Vol * 1000
R <- 1 + NS
S <- (1 + 10^(X - LogKi)) * KdDPM + Hot
a <- -R
b <- R * S + NS * Hot + Bmax
c <- -Hot * (S * NS + Bmax)
return((-b + sqrt(b^2 - 4 * a * c)) / (2 * a))
}
result_GP <- nls(
Y ~ binding_model(X, LogKi, Bmax, NS, Hot, KdNM, SpAct, Vol),
start = list(
LogKi = -5.0,
Bmax = 30000,
NS = 0.03
),
algorithm = "port"
)
summary(result_GP)
Output:
Formula: Y ~ binding_model(X, LogKi, Bmax, NS, Hot, KdNM, SpAct, Vol)
Parameters:
Estimate Std. Error t value Pr(>|t|)
LogKi -6.212e+00 9.316e-02 -66.685 < 2e-16 ***
Bmax 3.920e+04 2.644e+03 14.824 4.45e-09 ***
NS -1.403e-02 1.919e-02 -0.731 0.479
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1089 on 12 degrees of freedom
Algorithm "port", convergence message: relative convergence (4)
結果は Ki = 10^(-6.212 + 9) = 614 [nM]、Bmax = 39,200、NS = 0.01403。従来通りIC50値から変換した時よりもKiが2倍ほど大きい。
可視化:
concpre = seq(-9.5,-3.5, length=100) plot(Y~X,xlim=c(-10,-3.5),ylim=c(0,50000)) lines(concpre, predict(result_GP, newdata=list(X=concpre)))
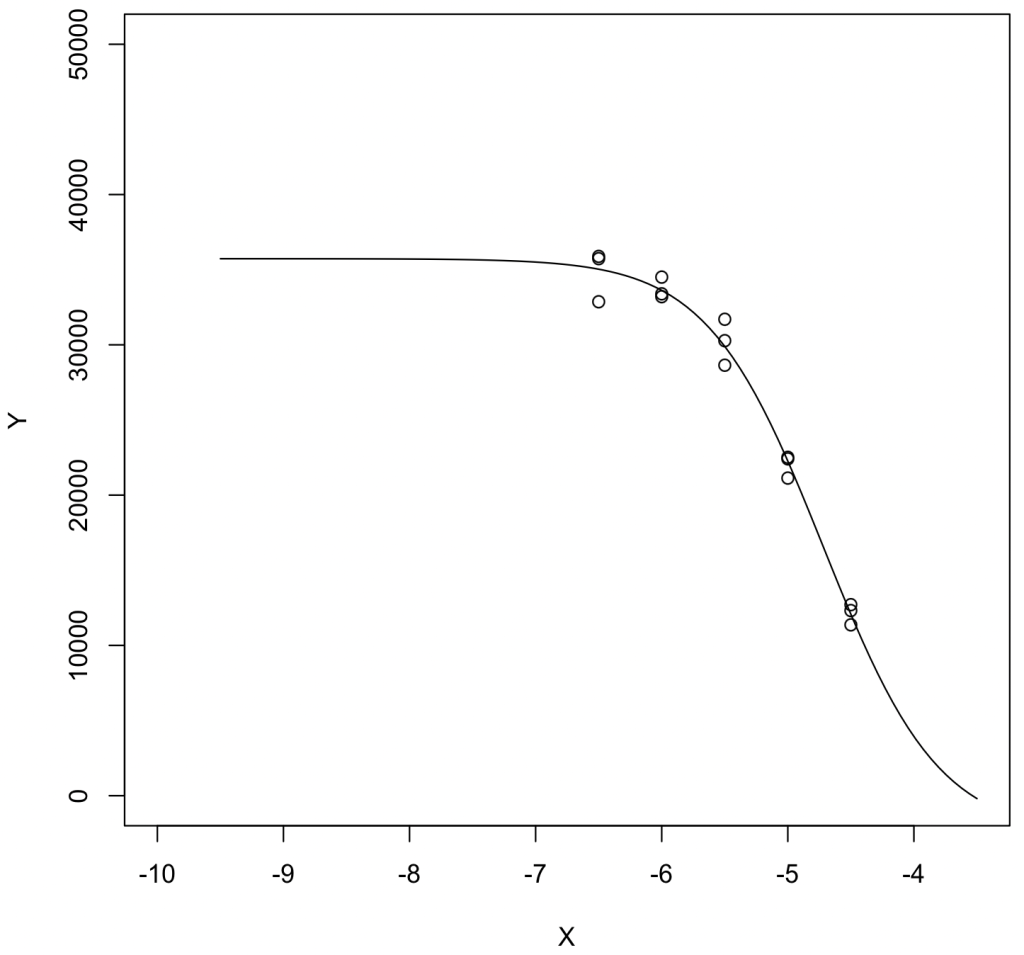
左右ともにPlateau領域のデータ点がないとPrismのデータ処理ではうまくいかないことが分かった。
Tight-binding ligand
3H標識リガンドの比活性は12.31 Ci/mmol。
| GROUP | log10 [I]T | pellet (dpm) | supernatant (dpm) (50 μL) |
| Total binding | — | 38985 | 10382 |
| Total binding | — | 38931 | 10907 |
| Total binding | — | 38495 | 9242 |
| Total binding | — | 39034 | 10287 |
| Nonspecific binding | — | 3629 | 14208 |
| Nonspecific binding | — | 3448 | 13194 |
| Unlabeled ligand (I) | -8.5 | 26327 | — |
| Unlabeled ligand (I) | -8.5 | 26072 | — |
| Unlabeled ligand (I) | -8.5 | 25105 | — |
| Unlabeled ligand (I) | -8 | 13168 | — |
| Unlabeled ligand (I) | -8 | 11354 | — |
| Unlabeled ligand (I) | -8 | 11917 | — |
| Unlabeled ligand (I) | -7.5 | 6314 | — |
| Unlabeled ligand (I) | -7.5 | 6446 | — |
| Unlabeled ligand (I) | -7.5 | 5829 | — |
処理したデータ
| GROUP | log10 [I]T | bound (nM) | free (nM) | θ | log10 {θ/(1 − θ)} |
| Total binding(平均) | — | 5.302 ([RL]0) | 13.05 ([L]0) | — | — |
| Unlabeled ligand (I) | -8.5 | 3.413 | — | 0.6438 | 0.257 |
| Unlabeled ligand (I) | -8.5 | 3.375 | — | 0.6365 | 0.243 |
| Unlabeled ligand (I) | -8.5 | 3.229 | — | 0.6090 | 0.193 |
| Unlabeled ligand (I) | -8 | 1.430 | — | 0.2698 | -0.432 |
| Unlabeled ligand (I) | -8 | 1.157 | — | 0.2182 | -0.554 |
| Unlabeled ligand (I) | -8 | 1.242 | — | 0.2342 | -0.515 |
| Unlabeled ligand (I) | -7.5 | 0.397 | — | 0.0750 | -1.091 |
| Unlabeled ligand (I) | -7.5 | 0.417 | — | 0.0787 | -1.068 |
| Unlabeled ligand (I) | -7.5 | 0.324 | — | 0.0612 | -1.186 |
ロジスティック関数にフィッティングしてIC50を推定〔推奨〕
logIT <- c(-8.5,-8.5,-8.5,-8,-8,-8,-7.5,-7.5,-7.5) theta <- c(0.6438,0.6365,0.6090,0.2698,0.2182,0.2342,0.0750,0.0787,0.0612) result <- nls(theta~1/(1+exp(a*log(10)*(logIT - logIC50))),start = c(logIC50=-8.5, a=1)) summary(result)
Output:
Formula: theta ~ 1/(1 + exp(a * log(10) * (logIT - logIC50)))
Parameters:
Estimate Std. Error t value Pr(>|t|)
logIC50 -8.34075 0.01186 -703.26 < 2e-16 ***
a 1.41699 0.05829 24.31 5.08e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01991 on 7 degrees of freedom
Number of iterations to convergence: 5
Achieved convergence tolerance: 8.394e-06
confint(result, level=0.95)
Output:
2.5% 97.5%
logIC50 -8.369216 -8.313125
a 1.282066 1.563688
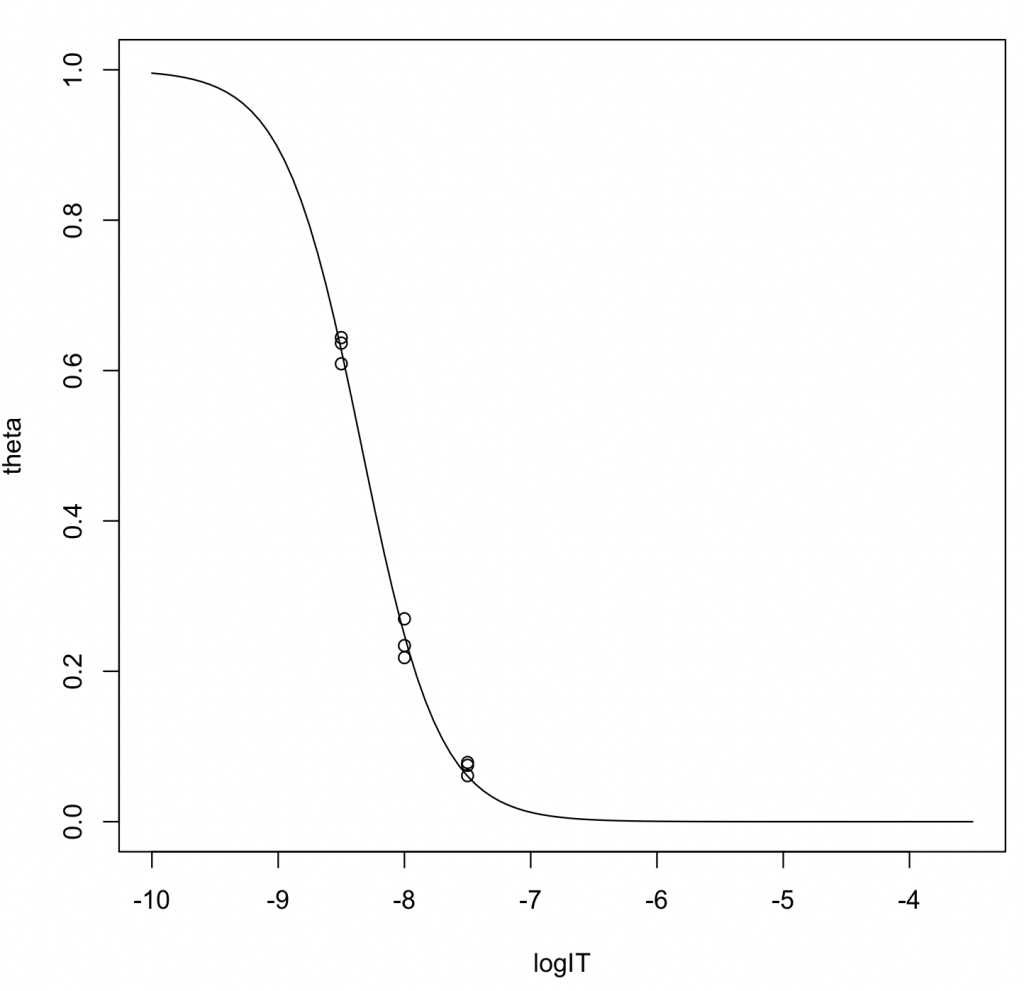
推定IC50値は4.560 nM(95%CI: 4.274–4.863)、ヒル係数は1.417だった。
Kiへの変換
以下の式で推定した\(\mathrm{IC}_{50}\)を\(K_\mathrm{i}\) に変換する。
$$ K_{\rm i} = \frac{\frac{1}{1 + k} \left[\mathrm{IC}_{50} - \left( 1 - \frac{1}{2} \frac{[L]_0}{[L]_{50}} \right)[R]_{\mathrm{T}} - \left( \frac{[L]_0}{[L]_{50}} - 1\right) \frac{[RL]_{0}}{2} \right] }{2\frac{[L]_{50}}{[L]_0} - 1 + \frac{[L]_{50}}{K_{\rm d}}} $$
得られた\(K_\mathrm{i}\) は 0.0561 nM(95% CI: 0.0471–0.0656)だった。
log10 {θ/(1 − θ)} 変換から線形回帰でIC50を推定〔次に推奨 ※Microsoft Excelしか使えない時〕
logIT <- c(-8.5,-8.5,-8.5,-8,-8,-8,-7.5,-7.5,-7.5) logit <- c(0.257,0.243,0.193,-0.432,-0.554,-0.515,-1.091,-1.068,-1.186) result_lm <- lm(logit ~ logIT) summary(result_lm)
Output:
Call:
lm(formula = logit ~ logIT)
Residuals:
Min 1Q Median 3Q Max
-0.09256 -0.05156 0.02944 0.04344 0.06644
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -11.22944 0.38820 -28.93 1.52e-08 ***
logIT -1.34600 0.04846 -27.77 2.01e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.05935 on 7 degrees of freedom
Multiple R-squared: 0.991, Adjusted R-squared: 0.9897
F-statistic: 771.4 on 1 and 7 DF, p-value: 2.014e-08
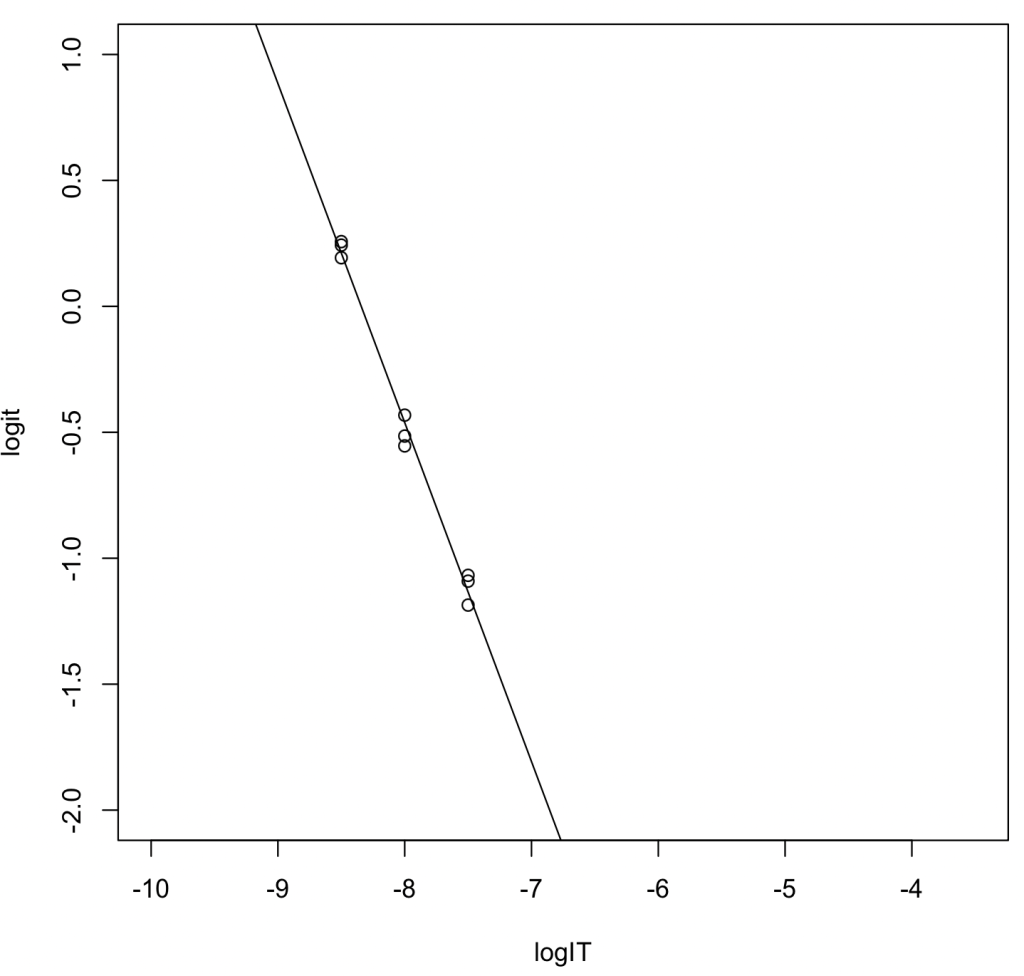
log10 IC50 = -11.22944/1.34600 = -8.342823。nMに変換すると4.541 nM。
推定IC50値は4.541 nM、前節と同じ式で変換したKi値は0.0555 nMだった。
GraphPad Prismの方法
パラメータ
- Hot = [L]T = 18.74 [nM] = 128050 [DPM]
- KdNM = Kd = 0.53 [nM]
- SpAct = 12.31 [Ci/mmol] = 27.3282 [dpm/fmol]
- Vol = 0.25 [mL]
X <- c(-8.5, -8.5, -8.5, -8, -8, -8, -7.5, -7.5, -7.5)
Y <- c(26327, 26072, 25105, 13168, 11354, 11917, 6314, 6446, 5829)
Hot <- 128050
KdNM <- 0.53
SpAct <- 27.3282
Vol <- 0.25
binding_model <- function(X, LogKi, Bmax, NS, Hot, KdNM, SpAct, Vol) {
KdDPM <- KdNM * SpAct * Vol * 1000
R <- 1 + NS
S <- (1 + 10^(X - LogKi)) * KdDPM + Hot
a <- -R
b <- R * S + NS * Hot + Bmax
c <- -Hot * (S * NS + Bmax)
return((-b + sqrt(b^2 - 4 * a * c)) / (2 * a))
}
result_GP <- nls(
Y ~ binding_model(X, LogKi, Bmax, NS, Hot, KdNM, SpAct, Vol),
start = list(
LogKi = -8.0,
Bmax = 30000,
NS = 0.03
),
algorithm = "port"
)
summary(result_GP)
Output:
Formula: Y ~ binding_model(X, LogKi, Bmax, NS, Hot, KdNM, SpAct, Vol)
Parameters:
Estimate Std. Error t value Pr(>|t|)
LogKi -1.069e+01 3.972e-01 -26.903 1.74e-07 ***
Bmax 1.510e+05 1.131e+05 1.335 0.2304
NS 2.424e-02 6.612e-03 3.667 0.0105 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 679 on 6 degrees of freedom
Algorithm "port", convergence message: both X-convergence and relative convergence (5)
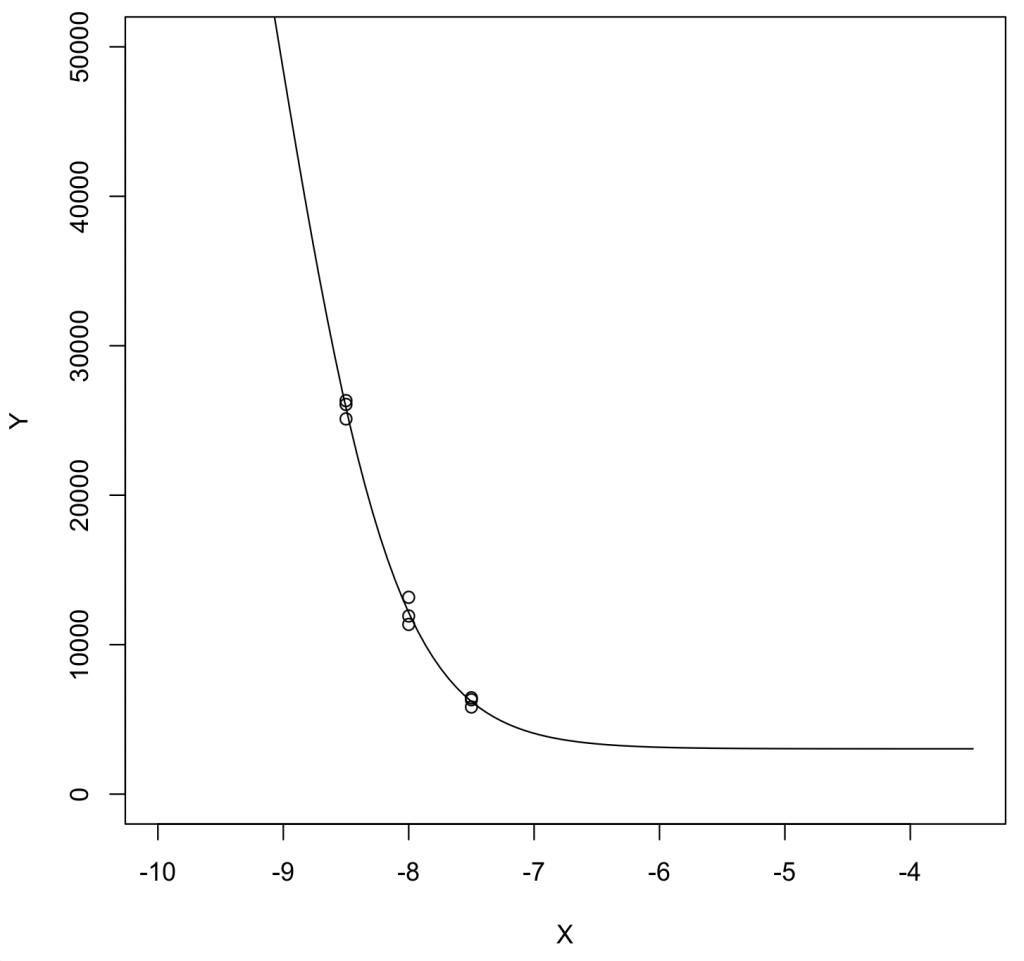
結果は Ki = 10^(-10.69 + 9) = 0.0204 [nM]、Bmax = 151,000、NS = 0.02424。Kiは小さ過ぎ、Bmax(= [R]T)は大き過ぎる。
可視化:
concpre = seq(-9.5,-3.5, length=100) plot(Y~X,xlim=c(-10,-3.5),ylim=c(0,50000)) lines(concpre, predict(result_GP, newdata=list(X=concpre)))