非線形の式を変形して、線形回帰を適用するのはやってはいけないという話は昔から知られていると思います。非線形の式を、線形に変換してパラメータを求める方法には、リガンド結合試験におけるScatchard(スキャッチャード)plot、酵素反応速度論におけるLineweaver–Burk(ラインウィーバー・バーク)plot、Eadie-Hofstee(イーディー・ホフステー)plot、Hanes–Woolf(ヘインズ・ウルフ)plotがあります。今では、これらの方法ははるかに正確な(かつ簡単に利用可能になった)非線形回帰に置き換えられており、データの視覚化目的以外では使用するべきではないとされています(自分の卒論では、詳しくなかったので、Hanes–Woolfプロットから酵素反応のKmとVmaxを求めていました)。
Avoid Scatchard, Lineweaver-Burke and similar transforms
Before nonlinear regression was readily available, the best way to analyze nonlinear data was to transform the data to create a linear graph, and then analyze the transformed data with linear regression. Examples include Lineweaver-Burke plots of enzyme kinetic data, Scatchard plots of binding data, and logarithmic plots of kinetic data. These methods are outdated, and should not be used to analyze data.
The problem with these methods is that the transformation distorts the experimental error. Linear regression assumes that the scatter of points around the line follows a Gaussian distribution and that the standard deviation is the same at every value of X. These assumptions are rarely true after transforming data. Furthermore, some transformations alter the relationship between X and Y. For example, in a Scatchard plot the value of X (bound) is used to calculate Y (bound/free), and this violates the assumption of linear regression that all uncertainty is in Y while X is known precisely. It doesn’t make sense to minimize the sum of squares of the vertical distances of points from the line, if the same experimental error appears in both X and Y directions.
非線形回帰が手軽に利用できるようになる以前は、非線形データを解析する最良の方法は、データを変換して直線のグラフを作成し、その変換されたデータを線形回帰で解析することでした。その例としては、酵素反応速度データのラインウィーバー・バークプロット、結合データのスキャッチャードプロット、反応速度データの対数プロットなどが挙げられます。これらの方法は時代遅れであり、データ解析に使用すべきではありません。
これらの方法の問題点は、変換によって実験誤差が歪められてしまうことです。線形回帰は、直線の周囲における点のばらつきがガウス分布に従うこと、そしてXのすべての値において標準偏差が同じであることを仮定しています。データを変換した後では、これらの仮定が成立することはめったにありません。さらに、変換の中にはXとYの関係を変えてしまうものもあります。例えば、スキャッチャードプロットではXの値(結合量)を用いてYの値(結合量/遊離量)を算出するため、これは「すべての不確実性はYにあり、Xは正確にわかっている」とする線形回帰の仮定に違反します。もし同じ実験誤差がXとYの両方向に現れるのであれば、点から直線までの垂直距離の二乗和を最小化することは理にかないません。
ここでは実際に得られる値にどれくらい差があるのかを調べたことはなかったのでやってみました。
Scatchard方程式とプロット
導出
受容体とリガンドの間で以下の平衡が成り立っているとします。
\[ [R] + [L] \rightleftharpoons [RL] \]
解離定数Kdは
\[ K_{\mathrm d} = \frac{[R][L]}{[RL]} \]
で、
\[ [R_{\mathrm T}] = [R] + [RL] \]
から、
\[ [RL] = \frac{[R_{\mathrm T}][L]}{K_{\mathrm d} + [L]} \]
となる。この式は酵素反応速度論のミカエリス・メンテン(Michaelis–Menten)式に相当する非線形の式です。
一方で、同じ式を変形すると、
\[ \frac{K_{\mathrm d}[RL]}{[L]} = -[RL] + [R_{\mathrm T}] \]
となり、両辺をKdで割ると、
\[ \frac{[RL]}{[L]} = -\frac{1}{K_{\mathrm d}}[RL] + \frac{[R_{\mathrm T}]}{K_{\mathrm d}} \]
となり、Scatchard(スキャッチャード)方程式となります。この式はミカエリス・メンテン式の線形表現の1つであるイーディー–ホフステー(Eadie–Hofstee)図に相当します。
この式から、[RL](x軸)に対して [RL]/[L](y軸)をプロットして線形回帰すると、傾きが−1/Kd、x軸切片が [RT] の直線が得られます。このプロットの特徴として、リガンドに対する親和性が異なる複数の結合部位が存在する時は、プロットは直線ではなく、下に凸の曲線になります(スキャッチャード解析)。
パラメータを求めるためであれば、Scatchard plotよりもHanes-Woolf plot型の
\[ \frac{[L]}{[RL]} = \frac{1}{[R_{\mathrm T}]}[L] + \frac{K_{\mathrm d}}{[R_{\mathrm T}]} \]
の方が正確ですが、このプロットからは親和性の異なる複数の結合部位が存在することを読み取るのは困難です。
問題点
Scatchard plotの問題点としては、x座標([RL])とy座標([RL]/[L])が独立変数になっていない(どちらにも [RL] が含まれている)ため、最小二乗法が本来適用できないこと(最小二乗法はx座標が説明変数〈実験誤差を含まない〉、y座標が目的変数〈実験誤差を含む〉であることを想定している)や適合度の指標である相関係数を適用できないこと、そもそも直接パラメータを推定するのではなく間接的、外挿で求めていることなどが挙げられます。
そのため、論文では大抵、結合飽和プロットの横か中に小さくScatchard plotを載せてあります(例: Braun (2005))。
練習問題
以下のURLにアーカイブされている講義資料の練習問題を解いてみました。
“Mg2+とADPは1対1の錯体を形成する。結合実験において、ADPの総濃度は80 µMに一定に保たれている。以下の表のデータから解離定数Kdを求めなさい。”
| Total Mg2+ (µM) | Mg2+ bound to ADP (µM) |
| 20 | 11.6 |
| 50 | 26.0 |
| 100 | 42.7 |
| 150 | 52.8 |
| 200 | 59.0 |
| 400 | 69.5 |
まず、[RL] = [RT][L]/(Kd + [L]) から、[L] = Kd の時に [RL] = [RT]/2 = 40 µMとなるので、おおよそのKdの値の見当が付きます。
Rプログラムを使用して解析します。
# Rソフトウェア
> TotalMg = c(20, 50, 100, 150, 200, 400) #Total Mg2+
> B = c(11.6, 26.0, 42.7, 52.8, 59.0, 69.5) #Bound Mg2+。式中の [RL]。
> F = TotalMg - B #Free Mg2+。式中の [L]。
# 非線形回帰
> result_nonlinear = nls(B ~ Rt*F/(Kd + F), start=c(Rt=10, Kd=10))
> summary(result_nonlinear)
Formula: B ~ Rt * F/(Kd + F)
Parameters:
Estimate Std. Error t value Pr(>|t|)
Rt 79.92642 0.08296 963.5 6.96e-12 ***
Kd 49.86861 0.15975 312.2 6.32e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.05816 on 4 degrees of freedom
Number of iterations to convergence: 5
Achieved convergence tolerance: 1.579e-06
> confint(result_nonlinear)
Waiting for profiling to be done...
2.5% 97.5%
Rt 79.69637 80.15752
Kd 49.42630 50.31459
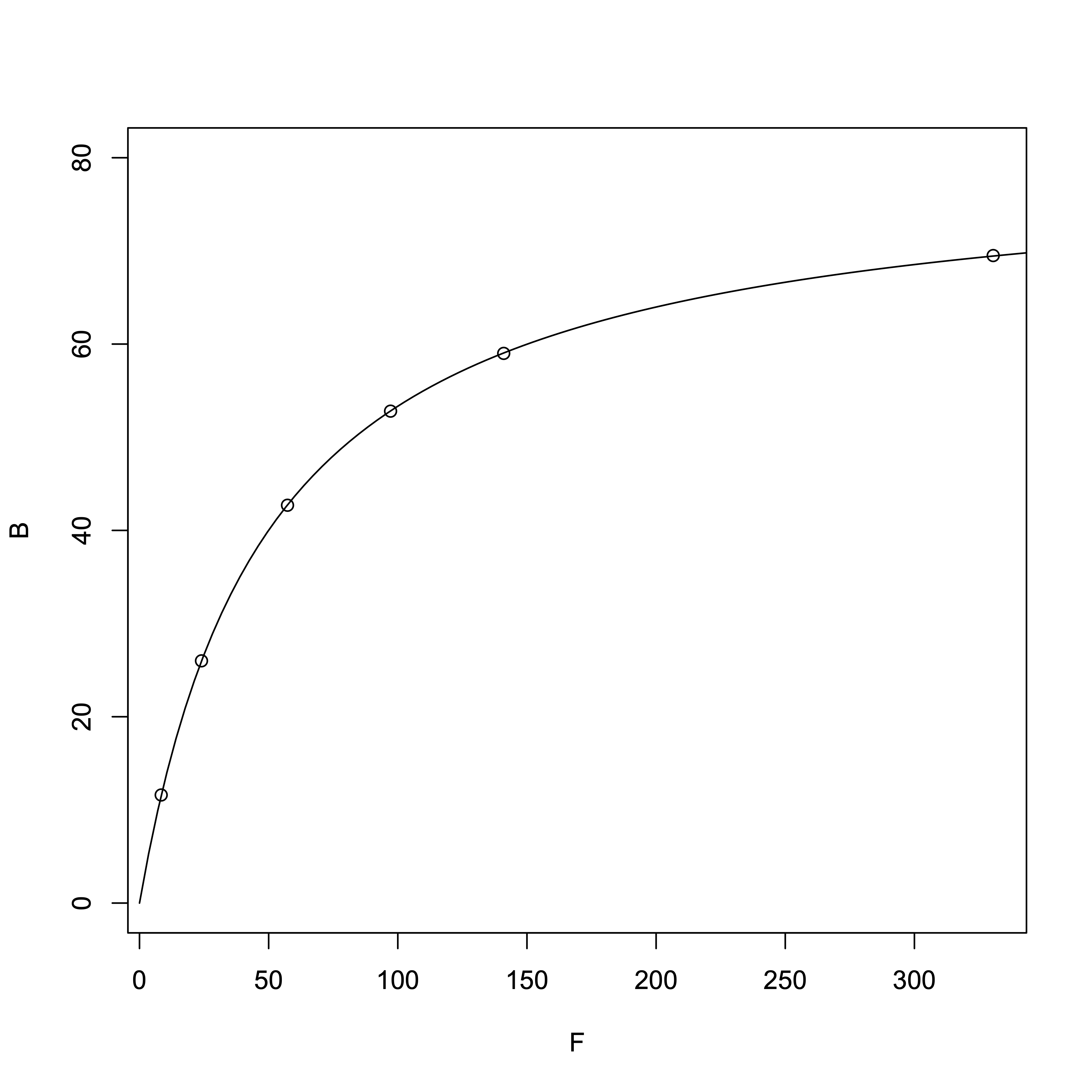
非線形回帰で求めた解離定数Kd = 49.87 µM, [RT] = 79.93 µMでした。Rtに80を代入して非線形回帰すると、Kd = 49.99 µMでした。
次に、Scatchard plotからKd と [RT] を求めます。
# Rソフトウェア
> result_linear = lm(B/F ~ B)
> summary(result_linear)
Call:
lm(formula = B/F ~ B)
Residuals:
1 2 3 4 5 6
0.0038911 -0.0026571 -0.0032285 -0.0010654 -0.0005134 0.0035734
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.6115350 0.0033919 475.1 1.18e-10 ***
B -0.0202132 0.0000709 -285.1 9.08e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.00342 on 4 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 0.9999
F-statistic: 8.128e+04 on 1 and 4 DF, p-value: 9.081e-10
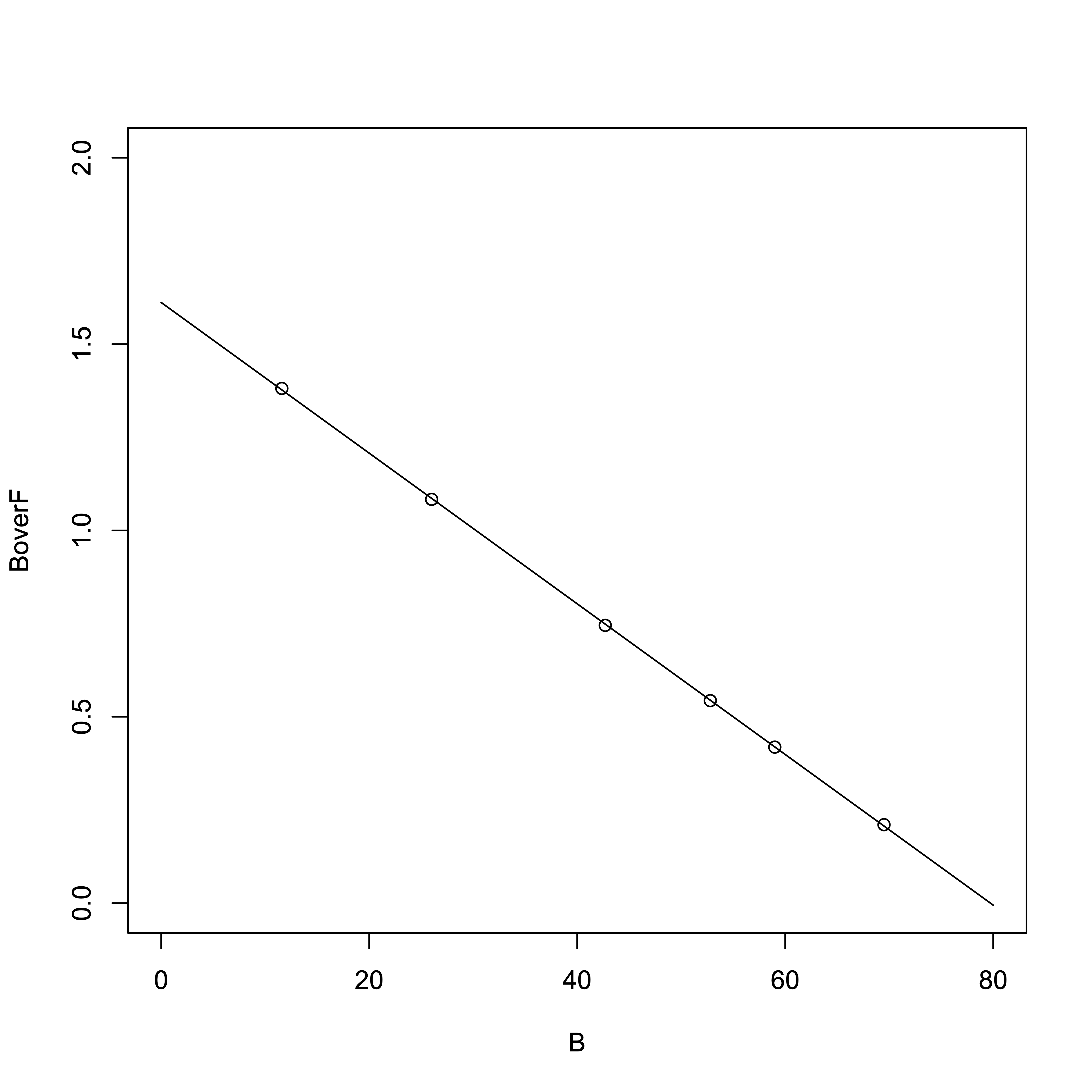
回帰直線の傾き −1/Kd = -0.0202132、[RT](x切片)= −y切片/傾き = 1.6115350/0.0202132 から、Kd = 49.47 µM、[RT] = 79.72 µM と求まりました。
この練習問題は解離定数Kd = 50 µMを使って各点の値が出されているのですが、Bound Mg2+ の値を丸めた時の誤差で、非線形回帰とScatchard法で得られたKd値と [RT] 値に差が出ているようです。小数点以下第2位まで使って計算すれば、非線形回帰でKd = 49.99、Scatchard法でKd = 49.97と理論通りに値が求まります。
実データ
上の理想的な値を使った練習問題では非線形回帰とScatchard plotでほとんど違いはありませんでしたが、実際の実験データではどうなるか試してみました。
> B = c(0.729,0.805,0.748,1.328,1.317,1.314,1.905,1.936,1.851,2.546,2.414,2.355) #単位はnM
> F = c(6.102,5.532,5.490,10.448,11.710,11.092,22.863,24.570,24.401,48.750,46.621,46.682) #単位はnM
> result = nls(B~Rt*F/(Kd+F),start=c(Rt=3,Kd=0.2))
> summary(result)
Formula: B ~ Rt * F/(Kd + F)
Parameters:
Estimate Std. Error t value Pr(>|t|)
Rt 3.3825 0.1127 30.01 3.95e-11 ***
Kd 18.3799 1.4360 12.80 1.59e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.06848 on 10 degrees of freedom
Number of iterations to convergence: 6
Achieved convergence tolerance: 1.785e-07
> confint(result) #95%信頼区間
Waiting for profiling to be done...
2.5% 97.5%
Rt 3.148358 3.652665
Kd 15.470323 21.906326
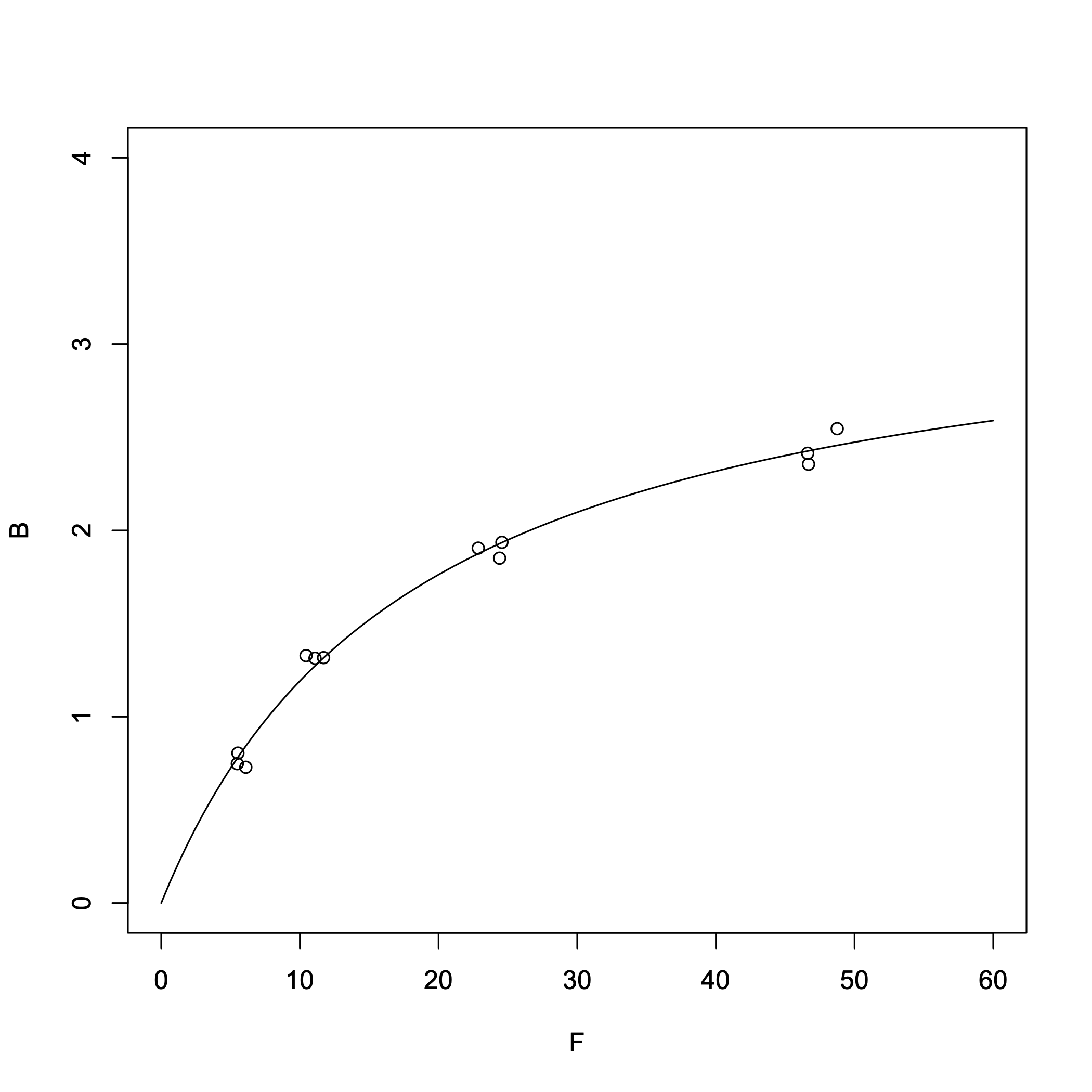
非線形回帰で求めた解離定数Kd = 18.4 nM, [RT] = 3.38 nMでした。
> result_lm = lm(B/F ~ B)
> summary(result_lm)
Call:
lm(formula = B/F ~ B)
Residuals:
Min 1Q Median 3Q Max
-0.0207551 -0.0043123 0.0007946 0.0048720 0.0171733
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.177090 0.008028 22.06 8.21e-10 ***
B -0.050571 0.004659 -10.85 7.46e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01015 on 10 degrees of freedom
Multiple R-squared: 0.9218, Adjusted R-squared: 0.9139
F-statistic: 117.8 on 1 and 10 DF, p-value: 7.464e-07
> confint(result_lm)
2.5 % 97.5 %
(Intercept) 0.15920357 0.1949766
B -0.06095189 -0.0401892
> -1/result_lm$coefficients[2]
B
19.77436
> -result_lm$coefficients[1]/result_lm$coefficients[2]
(Intercept)
3.501842
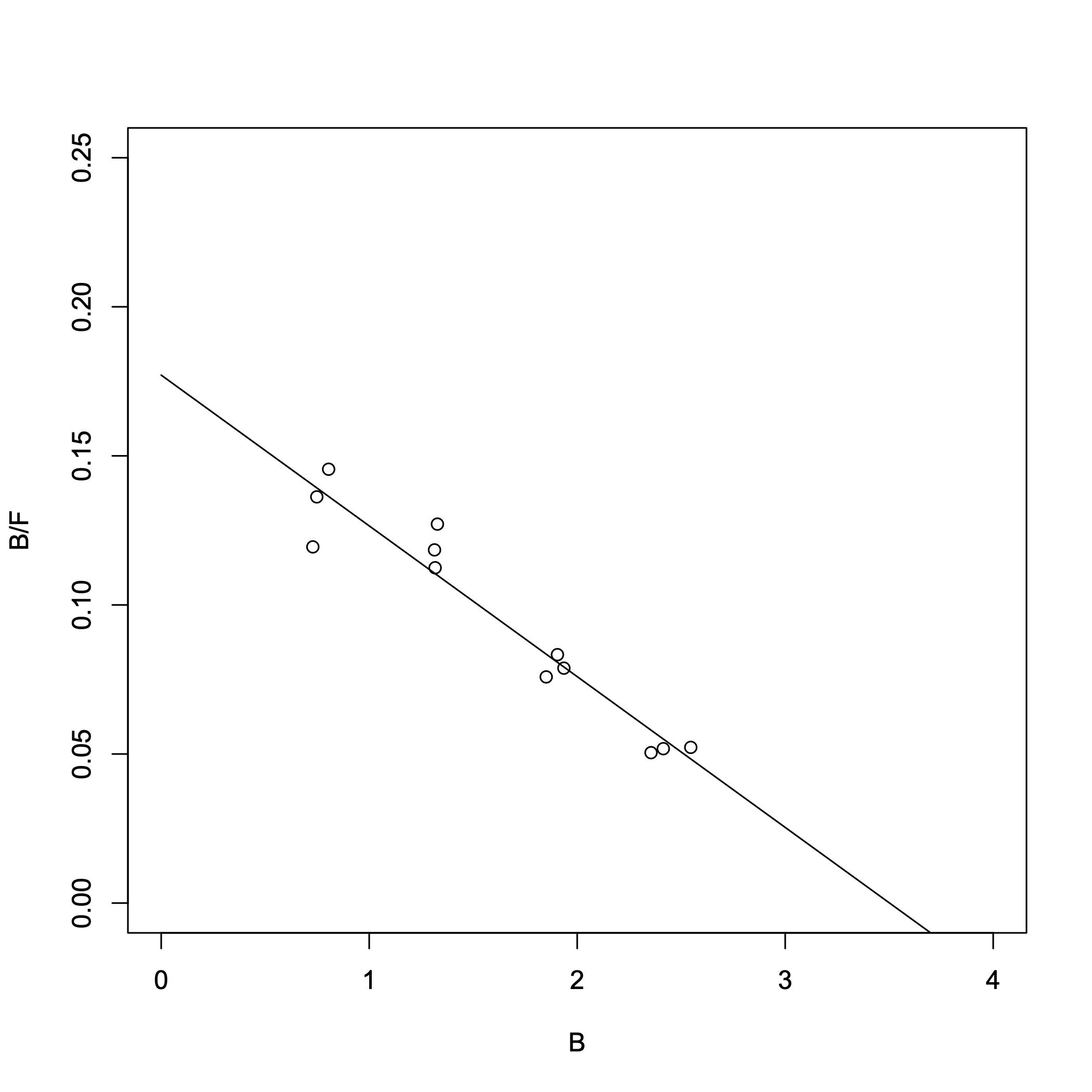
低濃度側の2つのB/F値の範囲が重なってしまっています(Fの逆数を使うため、誤差が大きく増幅されている)。Scatchard plotから求めた解離定数Kd = 19.8 nM, [RT] = 3.50 nMでした。非線形回帰で求めた値と比較するとKd は約8%、[RT] は約4%大きい値でした。
解離定数Kdの95%信頼区間を比べると、非線形回帰ではKd = 18.4 (95% CI: 15.5–21.9)、スキャッチャードプロットではKd = 19.8 (95% CI: 16.4–24.9) でした。
References
- Braun, Derek C.; Garfield, Susan H.; Blumberg, Peter M. “Analysis by Fluorescence Resonance Energy Transfer of the Interaction between Ligands and Protein Kinase Cδ in the Intact Cell”. J. Biol. Chem. 2005, 280(9), 8164-8171. doi: 10.1074/jbc.M413896200
- Scatchard, George “The Attraction of Proteins for Small Molecules and Ions”. Annals of the New York Academy of Sciences 1949, 51(4), 660–672. doi: 10.1111/j.1749-6632.1949.tb27297.x.